હોમ / મઠ / સંભાવના /વિવિધતા

ભિન્નતા

સંભાવના અને આંકડામાં, રેન્ડમ ચલનું ભિન્નતા એ સરેરાશ મૂલ્યથી ચોરસ અંતરનું સરેરાશ મૂલ્ય છે. તે કેવી રીતે રેન્ડમ વેરીએબલને સરેરાશ મૂલ્યની નજીક વહેંચવામાં આવે છે તે રજૂ કરે છે. નાના તફાવત સૂચવે છે કે રેન્ડમ ચલ સરેરાશ મૂલ્યની નજીક વહેંચાયેલું છે. મોટા તફાવત સૂચવે છે કે રેન્ડમ ચલ સરેરાશ મૂલ્યથી દૂર વહેંચાયેલું છે. ઉદાહરણ તરીકે, સામાન્ય વિતરણ સાથે, સાંકડી બેલ વળાંકમાં નાના તફાવત હશે અને પહોળા બેલ વળાંકમાં મોટો ભિન્નતા હશે.

વિવિધતા વ્યાખ્યા

રેન્ડમ વેરીએબલ X નું ભિન્નતા એ X ના તફાવતનાં ચોરસનું અપેક્ષિત મૂલ્ય અને અપેક્ષિત મૂલ્ય μ છે.

σ ² = વાર ( એક્સ ) = ઇ [( એક્સ - μ ) ² ]

વિવિધતાની વ્યાખ્યામાંથી આપણે મેળવી શકીએ છીએ

σ ² = વાર ( એક્સ ) = ઇ ( એક્સ ² ) - μ ²

સતત રેન્ડમ ચલની વિવિધતા

સરેરાશ મૂલ્ય with અને સંભાવના ઘનતા ફંક્શન એફ (એક્સ) સાથે સતત રેન્ડમ ચલ માટે:

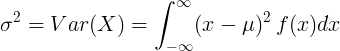
$\ સિગ્મા ^ 2 = વાર (એક્સ) = \ પૂર્ણાંક _ {- ty ઇન્ફ્ટી} ^ {\ ઇન્ફ્ટી} (x- \ mu) ^ 2 \: f (x) dx$

અથવા

$વર (X) = \ ડાબી [\ પૂર્ણા _ {- ty infty} ^ {\ infty} x ^ 2 \: f (x) dx \ right] - \ mu ^ 2$

સ્વતંત્ર રેન્ડમ ચલની વિવિધતા

સરેરાશ મૂલ્ય with અને સંભવિત માસ ફંક્શન પી (x) સાથેના સ્વતંત્ર રેન્ડમ ચલ X માટે:

$\ સિગ્મા ^ 2 = વાર (એક્સ) = \ સમ_ {હું} ^ {} (x_i- \ mu _X) ^ 2P_X (x_i)$

અથવા

$વર (X) = \ ડાબી [\ રકમ_ {i} ^ {} x_i ^ 2 પી (x_i) \ અધિકાર] - \ મ્યુ ^ 2$

વિવિધતાના ગુણધર્મો

જ્યારે એક્સ અને વાય સ્વતંત્ર રેન્ડમ ચલો હોય ત્યારે:

વાર ( એક્સ + વાય ) = વાર ( એક્સ ) + વાર ( વાય )

માનક વિચલન ►

આ પણ જુઓ

સંભાવના અને આંકડા

ઝડપી ટેબલ્સ