સંભાવના વિતરણ
સંભાવના અને આંકડા વિતરણ એ રેન્ડમ ચલની લાક્ષણિકતા છે, દરેક મૂલ્યમાં રેન્ડમ ચલની સંભાવના વર્ણવે છે.
દરેક વિતરણમાં ચોક્કસ સંભાવના ઘનતા કાર્ય અને સંભાવના વિતરણ કાર્ય હોય છે.
સંભાવના વિતરણોની અનિશ્ચિત સંખ્યા હોવા છતાં, ઉપયોગમાં ઘણાં સામાન્ય વિતરણો છે.
સંચિત વિતરણ કાર્ય
સંભાવના વિતરણ એ સંચિત વિતરણ ફંક્શન એફ (એક્સ) દ્વારા વર્ણવેલ છે,
જે રેન્ડમ વેરીએબલ X ની સંભાવના છે જે x કરતા નાના અથવા તેના સમાન મૂલ્ય મેળવશે:
F ( x ) = P ( X ≤ x )
સતત વિતરણ
સંચિત વિતરણ ફંક્શન એફ (એક્સ) ની ગણતરી સતત રેન્ડમ ચલ X ની સંભાવના ઘનતા ફંક્શન f (યુ) ના એકીકરણ દ્વારા કરવામાં આવે છે.
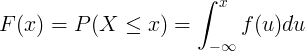
સ્વતંત્ર વિતરણ
સંચિત વિતરણ ફંક્શન એફ (એક્સ) ની ગણતરી જુદી જુદી રેન્ડમ વેરિયેબલ X ની સંભાવના માસ ફંક્શન પી (યુ) ના સારાંશ દ્વારા કરવામાં આવે છે.
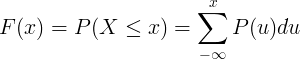
સતત વિતરણ કોષ્ટક
સતત વિતરણ એ સતત રેન્ડમ ચલનું વિતરણ છે.
સતત વિતરણનું ઉદાહરણ
...
સતત વિતરણ કોષ્ટક
| વિતરણ નામ | વિતરણ પ્રતીક | સંભાવના ઘનતા કાર્ય (પીડીએફ) | મીન | ભિન્નતા |
|---|---|---|---|---|
| એફ એક્સ ( એક્સ ) |
μ = ઇ ( એક્સ ) |
σ 2 = વાર ( એક્સ ) |
||
| સામાન્ય / ગૌસીઅન | X ~ N (μ, σ 2 ) |
|
μ | . 2 |
| યુનિફોર્મ | X ~ U ( a , b ) |
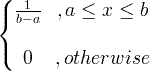 |
|
|
| ઘાતાંકીય | એક્સ ~ સમાપ્તિ (λ) | |
|
|
| ગામા | X ~ ગામા ( સી , λ) | 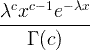 x / 0, સી / 0, λ/ 0 |
|
|
| ચી ચોરસ | X ~ χ 2 ( કે ) |
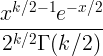 |
કે |
2 કે |
| વિશર્ટ | ||||
| એફ | X ~ F ( k 1 , k 2 ) |
|||
| બીટા | ||||
| વેઇબુલ | ||||
| લ Logગ-સામાન્ય | X ~ LN (μ, σ 2 ) |
|||
| રાયલે | ||||
| કાઉચી | ||||
| ડીરીચલેટ | ||||
| લેપલેસ | ||||
| લેવી | ||||
| ભાત | ||||
| વિદ્યાર્થીની ટી |
સ્વતંત્ર વિતરણ કોષ્ટક
સ્વતંત્ર વિતરણ એ એક સ્વતંત્ર રેન્ડમ ચલનું વિતરણ છે.
સ્વતંત્ર વિતરણનું ઉદાહરણ
...
સ્વતંત્ર વિતરણ કોષ્ટક
| વિતરણ નામ | વિતરણ પ્રતીક | સંભવિત સમૂહ કાર્ય (pmf) | મીન | ભિન્નતા | |
|---|---|---|---|---|---|
| f x ( k ) = P ( X = k ) કે = 0,1,2, ... |
ઇ ( એક્સ ) | વાર ( x ) | |||
| દ્વિપદી | X ~ બિન ( n , p ) |
|
એનપી |
એનપી (1- પી ) |
|
| પોઇસન | એક્સ ~ પોઇસન (λ) |
|
. ≥ 0 |
λ |
λ |
| યુનિફોર્મ | X ~ U ( a, b ) |
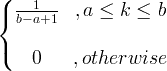 |
|
|
|
| ભૌમિતિક | એક્સ ~ જિઓમ ( પી ) |
|
|
|
|
| હાયપર-ભૌમિતિક | X ~ HG ( N , K , n ) |
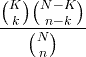 |
એન = 0,1,2, ... કે = 0,1, .., એન n = 0,1, ..., એન |
|
|
| બર્નોલી | એક્સ ~ બર્ન ( પી ) |
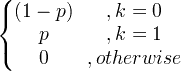 |
પી |
પી (1- પી ) |
|
આ પણ જુઓ
સંભાવના અને આંકડા
ઝડપી ટેબલ્સ