આર્કોકોસ (એક્સ) ફંક્શન
આર્કોકોસ (x), કોસ -1 (x), verseલટું કોસાઇન ફંક્શન.
આર્કોકોઝ વ્યાખ્યા
X ની આર્કોકોસીન જ્યારે -1≤x≤1 હોય ત્યારે x ના વિપરીત કોસાઇન ફંક્શન તરીકે વ્યાખ્યાયિત કરવામાં આવે છે .
જ્યારે વાયનું કોસાઇન, x ની બરાબર હોય:
કોસ વાય = એક્સ
પછી x નો આર્કોઝિન, x ના વિપરીત કોસાઇન ફંક્શન જેટલો છે, જે y ની બરાબર છે:
આર્કોકોસ x = કોસ -1 એક્સ = વાય
(અહીં કોસ -1 x નો અર્થ વ્યસ્ત કોસાઇન છે અને તેનો અર્થ કોસાઇનનો અર્થ -1 ની શક્તિનો નથી).
ઉદાહરણ
આર્કોકોસ 1 = કોસ -1 1 = 0 રેડ = 0 °
આર્કોકોસનો ગ્રાફ
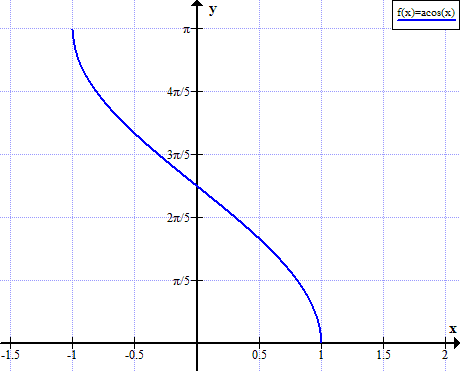
આર્કોકોસ નિયમો
| નિયમ નામ | નિયમ |
|---|---|
| આર્કોઝિનનો કોઝિન | કોસ (આર્કોકોસ એક્સ ) = એક્સ |
| કોસાઇનનો આર્કોઝિન | આર્ક્કોસ (કોસ એક્સ ) = x + 2 કે π, જ્યારે કે ∈ℤ ( કે પૂર્ણાંક છે) |
| નકારાત્મક દલીલના આર્કોકોસ | આર્ક્કોસ (- x ) = π - આર્કોકોસ x = 180 ° - આર્કોકોસ એક્સ |
| પૂરક કોણ | આર્કોકોસ x = π / 2 - આર્કસીન x = 90 ° - આર્કસીન એક્સ |
| આર્કોકોસનો સરવાળો | આર્ક્કોસ ( α ) + આર્કોકોસ ( β ) = આર્કોકોસ ( αβ - √ (1- α 2 ) (1- β 2 ) ) |
| આર્કોકોસ તફાવત | આર્કોકોસ ( α ) - આર્કોકોસ ( β ) = આર્કોકોસ ( αβ + √ (1- α 2 ) (1- β 2 ) ) |
| X ના પાપના આર્કોકોસ | આર્કોકોસ (સિન એક્સ ) = - એક્સ - (2 કે +0.5) π |
| આર્કોઝિનનો સાઇન | |
| આર્કોકોસીનનું ટેન્જેન્ટ |  |
| આર્કોઝિનનું વ્યુત્પન્ન | 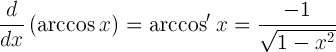 |
| આર્કોઝિનનું અનંત અવિભાજ્ય | |
આર્કોકોસ ટેબલ
| x | આર્કોકોસ (એક્સ) (ર radડ) |
આર્કોકોસ (એક્સ) (°) |
|---|---|---|
| -1 | π | 180 ° |
| -√ 3 /2 | 5π / 6 | 150 ° |
| -√ 2 /2 | 3π / 4 | 135 ° |
| -1/2 | 2π / 3 | 120 ° |
| 0 | π / 2 | 90 ° |
| 1/2 | π / 3 | 60 ° |
| √ 2 /2 | π / 4 | 45 ° |
| √ 3 /2 | π / 6 | 30 ° |
| 1 | 0 | 0 ° |
આ પણ જુઓ
- કોઝિન ફંક્શન
- આર્કસાઇન ફંક્શન
- આર્ટકનફંક્શન
- આર્ક્કોસ કેલ્ક્યુલેટર
- રેડિયનથી ડિગ્રી કન્વર્ટર
- 0 ના આર્કોકોસ
- Ar નો આર્કોસ
- 2 ના આર્કોકોસ
- 3 ના આર્કોકોસ
- કોસના આર્કોકોસ
- પાપના આર્કોકોસ
- આર્ક્કોસ ડેરિવેટિવ
- આર્કોકોસ ગ્રાફ
- આર્કોસના કોસ
- આર્કોઝનો પાપ
- આર્કોસનો તન