מספר אפס (0)

הגדרת מספר אפס

אפס הוא מספר המשמש במתמטיקה לתיאור שום כמות או כמות אפסית.

כשיש 2 תפוחים על השולחן ואנחנו לוקחים את 2 התפוחים, אנחנו יכולים לומר שיש אפס תפוחים על השולחן.

המספר האפס אינו המספר החיובי ולא המספר השלילי.

האפס הוא גם ספרת מציין מיקום במספרים אחרים (למשל: 40,103, 170).

האם אפס הוא מספר?

אפס הוא מספר. זה לא מספר חיובי ולא שלילי.

ספרת אפס

ספרת האפס משמשת כמציין מיקום בעת כתיבת מספרים.

לדוגמה:

204 = 2 × 100 + 0 × 10 + 4 × 1

היסטוריית מספרים אפסית

מי המציא את המספר האפס?

סמל ה- 0 המודרני הומצא בהודו במאה ה -6 ושימש מאוחר יותר על ידי הפרסים והערבים ומאוחר יותר באירופה.

סמל של אפס

המספר האפס מסומן בסמל 0 .

המערכת הספרה בערבית משתמשת בסמל 0.

מאפייני מספר אפס

x מייצג כל מספר.

פעולה כְּלָל דוגמא
חיבור

x + 0 = x

3 + 0 = 3
חִסוּר

x - 0 = x

3 - 0 = 3
כֶּפֶל

x × 0 = 0

5 × 0 = 0
חֲלוּקָה

0 ÷ x = 0 , כאשר x ≠ 0

0 ÷ 5 = 0

x ÷ 0  אינו מוגדר

5 ÷ 0 אינו מוגדר
התפשטות

0 x = 0

0 5 = 0

x 0 = 1

5 0 = 1
שורש

√ 0 = 0

  
לוֹגָרִיתְם

יומן b (0) אינו מוגדר

  
\ lim_ {x \ rightarrow 0 ^ +} \ textup {log} _b (x) = - \ infty  
פקטוריאל

0! = 1

  
סינוס

חטא 0º = 0

  
קוסינוס

cos 0º = 1

  
מַשִׁיק

שזוף 0º = 0

  
נגזר

0 '= 0

  
בלתי נפרד

D 0 d x = 0 + C.

  
 

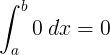תוספת אפסית

תוספת של מספר בתוספת אפס שווה למספר:

x + 0 = x

לדוגמה:

5 + 0 = 5

אפס חיסור

חיסור של מספר פחות אפס שווה למספר:

x - 0 = x

לדוגמה:

5 - 0 = 5

כפל באפס

הכפל של מספר פעמים אפס שווה לאפס:

x × 0 = 0

לדוגמה:

5 × 0 = 0

המספר חלקי אפס

חלוקת מספר באפס אינה מוגדרת:

x ÷ 0 אינו מוגדר

לדוגמה:

5 ÷ 0 אינו מוגדר

אפס מחולק במספר

חלוקת אפס במספר היא אפס:

0 ÷ x = 0

לדוגמה:

0 ÷ 5 = 0

מספר לכוח האפס

כוחו של מספר שהועלה באפס הוא אחד:

x 0 = 1

לדוגמה:

5 0 = 1

לוגריתם של אפס

לוגריתם הבסיס b של אפס אינו מוגדר:

יומן b (0) אינו מוגדר

אין מספר שאנחנו יכולים להעלות איתו את הבסיס b כדי לקבל אפס.

רק הגבול של לוגריתם הבסיס של x, כאשר x מתכנס לאפס הוא מינוס אינסוף:

\ lim_ {x \ rightarrow 0 ^ +} \ textup {log} _b (x) = - \ infty

סטים המכילים אפס

אפס הוא מרכיב של המספרים הטבעיים, המספרים השלמים, המספרים האמיתיים וקבוצות המספרים המורכבות:

סט הגדר סימון חברות
מספרים טבעיים (לא שליליים) 0 ∈ ℕ 0
מספרים שלמים 0 ∈ ℤ
מספרים אמיתיים 0 ∈ ℝ
מספרים מסובכים 0 ∈ ℂ
מספר רציונלי 0 ∈ ℚ

האם אפס מספר זוגי או אי זוגי?

קבוצת המספרים הזוגיים היא:

{..., -10, -8, -6, -4, -2, 0, 2, 4, 6, 8, 10, ...}

קבוצת המספרים האי-זוגיים היא:

{..., -9, -7, -5, -3, -1, 1, 3, 5, 7, 9, ...}

אפס הוא מכפיל שלם של 2:

0 × 2 = 0

אפס הוא חבר במספרים הזוגיים:

0 ∈ {2 k , k ∈ℤ}

אז אפס הוא מספר זוגי ולא מספר אי זוגי.

האם אפס הוא מספר טבעי?

ישנן שתי הגדרות עבור המספרים הטבעיים שנקבעו.

קבוצת המספרים השלמים שאינם שליליים:

ℕ 0 = {0,1,2,3,4,5,6,7,8, ...}

קבוצת המספרים השלמים החיוביים:

ℕ 1 = {1,2,3,4,5,6,7,8, ...}

אפס הוא חבר בקבוצת המספרים השלמים שאינם שליליים:

0 ∈ ℕ 0

אפס אינו חבר בקבוצת המספרים השלמים החיוביים:

0 ∉ ℕ 1

האם אפס הוא מספר שלם?

ישנן שלוש הגדרות למספרים השלמים:

קבוצת המספרים השלמים:

ℤ = {0,1,2,3,4,5,6,7,8, ...}

קבוצת המספרים השלמים שאינם שליליים:

ℕ 0 = {0,1,2,3,4,5,6,7,8, ...}

קבוצת המספרים השלמים החיוביים:

ℕ 1 = {1,2,3,4,5,6,7,8, ...}

אפס הוא חבר בקבוצת המספרים השלמים ובקבוצת המספרים השלמים שאינם שליליים:

0 ∈ ℤ

0 ∈ ℕ 0

אפס אינו חבר בקבוצת המספרים השלמים החיוביים:

0 ∉ ℕ 1

האם אפס הוא מספר שלם?

קבוצת המספרים השלמים:

ℤ = {0,1,2,3,4,5,6,7,8, ...}

אפס הוא חבר בקבוצת המספרים השלמים:

0 ∈ ℤ

אז אפס הוא מספר שלם.

האם אפס הוא מספר רציונלי?

מספר רציונלי הוא מספר שיכול לבוא לידי ביטוי כמרכיב של שני מספרים שלמים:

ℚ = { n / m ; n , m ∈ℤ}

ניתן לכתוב אפס כמנה של שני מספרים שלמים.

לדוגמה:

0 = 0/3

אז אפס הוא מספר רציונלי.

האם אפס הוא מספר חיובי?

מספר חיובי מוגדר כמספר הגדול מאפס:

x / 0

לדוגמה:

5/ 0

מכיוון שאפס אינו גדול מאפס, אין זה מספר חיובי.

האם אפס הוא מספר ראשוני?

המספר 0 אינו מספר ראשוני.

אפס אינו מספר חיובי ויש לו אינסוף מחלקים.

המספר הראשוני הנמוך ביותר הוא 2.

 

ראה גם

מספרים
שולחנות מהירים