פונקציית Arccos (x)
Arccos (x), cos -1 (x), פונקציה קוסינוס הפוכה .
הגדרת Arccos
הארקוזין של x מוגדר כפונקציה הקוסינוס ההפוך של x כאשר -1≤x≤1.
כאשר הקוסינוס של y שווה ל- x:
cos y = x
ואז הארקוזין של x שווה לתפקוד הקוסינוס ההפוך של x, השווה ל- y:
ארקוס x = cos -1 x = y
(כאן cos -1 x פירושו קוסינוס הפוך ואינו אומר קוסינוס בכוח -1).
דוגמא
ארקוס 1 = cos -1 1 = 0 rad = 0 °
גרף של ארקוסים
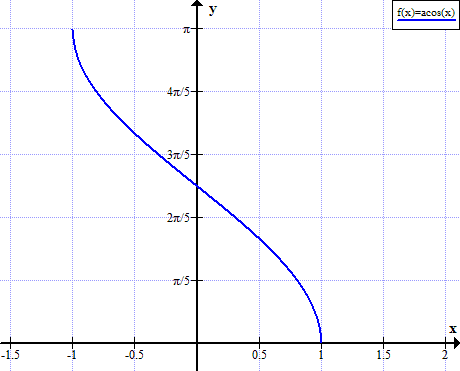
ארקוס שולט
| שם החוק | כְּלָל |
|---|---|
| קוסינוס של ארקוזין | cos (ארקוס x ) = x |
| ארקוזין של קוסינוס | ארקוס (cos x ) = x + 2 k π, כאשר k ∈ℤ ( k הוא מספר שלם) |
| Arccos של ויכוח שלילי | ארקוס (- x ) = π - ארקוס x = 180 ° - ארקוס x |
| זוויות משלימות | ארקוס x = π / 2 - קשת x = 90 ° - קשת x |
| סכום Arccos | ארקוס ( α ) + ארקוס ( β ) = ארקוס ( αβ - √ (1- α 2 ) (1- β 2 ) ) |
| ההבדל בארקוס | ארקוס ( α ) - ארקוס ( β ) = ארקוס ( αβ + √ (1- α 2 ) (1- β 2 ) ) |
| Arccos of sin of x | ארקוס (sin x ) = - x - (2 k +0.5) π |
| סינוס ארקוזין | |
| משיק של ארקוזין | 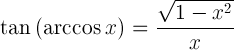 |
| נגזרת של ארקוזין | 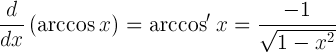 |
| אינטגרל בלתי מוגדר של ארקוזין | |
שולחן Arccos
| x | ארקוס (x) (rad) |
ארקוס (x) (°) |
|---|---|---|
| -1 | π | 180 ° |
| -√ 3 /2 | 5π / 6 | 150 מעלות |
| -√ 2 /2 | 3π / 4 | 135 ° |
| -1/2 | 2π / 3 | 120 ° |
| 0 | π / 2 | 90 ° |
| 1/2 | π / 3 | 60 מעלות |
| √ 2 /2 | π / 4 | 45 ° |
| √ 3 /2 | π / 6 | 30 מעלות |
| 1 | 0 | 0 ° |
ראה גם
- תפקוד קוסינוס
- תפקוד קשת
- תפקוד ארקטני
- מחשבון Arccos
- ממיר רדיאנים למעלות
- Arccos של 0
- Arccos של 1
- Arccos של 2
- Arccos של 3
- Arccos של cos
- Arccos של חטא
- נגזרת של Arccos
- גרף Arccos
- כיוון של ארקוס
- חטא של ארקוס
- שזוף של ארקוס