e állandó

Az állandó vagy Euler-szám matematikai állandó. Az e konstans valós és irracionális szám.

e = 2,718281828459 ...

Az e meghatározása
Az e tulajdonságai
Alap e logaritmus
Exponenciális függvény
Euler képlete

Az e meghatározása

Az e konstans a határérték:

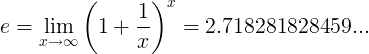
$e = \ lim_ {x \ rightarrow \ infty} \ bal (1+ \ frac {1} {x} \ right) ^ x = 2.718281828459 ...$

Alternatív meghatározások

Az e konstans a határérték:

$e = \ lim_ {x \ rightarrow 0} \ bal (1+ \ right x) ^ \ frac {1} {x}$

Az e konstans a végtelen sorozat:

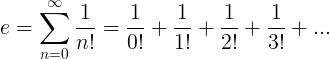
$e = \ sum_ {n = 0} ^ {\ infty} \ frac {1} {n!} = \ frac {1} {0!} + \ frac {1} {1!} + \ frac {1} { 2!} + \ Frac {1} {3!} + ...$

Az e tulajdonságai

Kölcsönös e

Az e reciproka a határ:

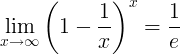
$\ lim_ {x \ rightarrow \ infty} \ bal (1- \ frac {1} {x} \ right) ^ x = \ frac {1} {e}$

Származékai e

Az exponenciális függvény deriváltja az exponenciális függvény:

( e ^x ) '= e ^x

A természetes logaritmusfüggvény deriváltja a reciprokfüggvény:

(log _e x ) '= (ln x )' = 1 / x

Az integrálok e

A határozatlan integrál az exponenciális függvény e ^x az exponenciális függvény e ^x .

∫ e ^x dx = e ^x + c

A log _e x természetes logaritmusfüggvény határozatlan integrálja :

∫ log _e x dx = ∫ ln x dx = x ln x - x + c

Az 1 / x reciprok függvény határozott integrálja 1-től e-ig: 1:

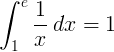
$\ int_ {1} ^ {e} \ frac {1} {x} \: dx = 1$

Alap e logaritmus

Az x szám természetes logaritmusa az x alap e logaritmusa:

ln x = log _e x

Exponenciális függvény

Az exponenciális függvény meghatározása a következő:

f ( x ) = exp ( x ) = e ^x

Euler képlete

Az e ^iθ komplex szám azonosítója:

e ^iθ = cos ( θ ) + i bűn ( θ )

i a képzeletbeli egység (-1 négyzetgyöke).

θ bármely valós szám.