Nulla szám (0)
Nulla számdefiníció
A nulla egy olyan szám, amelyet a matematikában nem mennyiség vagy null mennyiség leírására használnak.
Amikor 2 alma van az asztalon, és vesszük a 2 almát, akkor azt mondhatjuk, hogy nulla alma van az asztalon.
A nulla szám nem pozitív és nem negatív szám.
A nulla helyettesítő számjegy más számokban is (pl .: 40 103, 170).
A nulla szám?
A nulla egy szám. Nem pozitív és nem negatív szám.
Nulla számjegy
A nulla számjegy helyőrzőként szolgál számok írásakor.
Például:
204 = 2 × 100 + 0 × 10 + 4 × 1
Nulla számelőzmények
Ki találta ki a nulla számot?
A modern 0 szimbólumot Indiában találták ki a 6. században, később a perzsák és az arabok, majd később Európában használták.
A nulla szimbóluma
A nulla számot a 0 szimbólummal jelöljük .
Az arab számrendszer a ٠ szimbólumot használja.
Nulla szám tulajdonságai
x tetszőleges számot jelöl.
| Művelet | Szabály | Példa |
|---|---|---|
Kiegészítés |
x + 0 = x |
3 + 0 = 3 |
Kivonás |
x - 0 = x |
3 - 0 = 3 |
Szorzás |
x × 0 = 0 |
5 × 0 = 0 |
Osztály |
0 ÷ x = 0 , amikor x ≠ 0 |
0 ÷ 5 = 0 |
| x ÷ 0 nincs meghatározva |
5 ÷ 0 nincs meghatározva |
|
Hatványozás |
0 x = 0 |
0 5 = 0 |
| x 0 = 1 |
5 0 = 1 |
|
Gyökér |
√ 0 = 0 |
|
Logaritmus |
log b (0) nincs meghatározva |
|
| |
||
Faktoriális |
0! = 1 |
|
Szinusz |
sin 0º = 0 |
|
Koszinusz |
cos 0 ° = 1 |
|
Tangens |
barnulás 0 ° = 0 |
|
Derivált |
0 '= 0 |
|
Integrál |
∫ 0 d x = 0 + C |
|
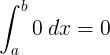 |
Nulla kiegészítés
Szám hozzáadása plusz nulla egyenlő a számmal:
x + 0 = x
Például:
5 + 0 = 5
Nulla kivonás
Egy szám mínusz nulla levonása megegyezik a számmal:
x - 0 = x
Például:
5 - 0 = 5
Szorzás nullával
A nulla szorzatának szorzata nulla:
x × 0 = 0
Például:
5 × 0 = 0
Szám osztva nullával
Egy szám nullával való osztása nincs meghatározva:
x ÷ 0 nincs meghatározva
Például:
5 ÷ 0 nincs meghatározva
Nulla osztva egy számmal
A nulla számmal való osztása nulla:
0 ÷ x = 0
Például:
0 ÷ 5 = 0
Szám a nulla teljesítményig
A nullával emelt szám hatványa egy:
x 0 = 1
Például:
5 0 = 1
A nulla logaritmusa
A nulla b b logaritmusa nincs meghatározva:
log b (0) nincs meghatározva
Nincs olyan szám, amellyel megemelhetnénk a b alapot, hogy nullát kapjunk.
Csak az x b b logaritmusának határa, amikor x nulla konvergál, mínusz a végtelen:
![]()
Nullát tartalmazó halmazok
A nulla a természetes számok, az egész számok, a valós számok és a komplex számok halmazának eleme:
| Set | Állítsa be a tagság jelölését |
|---|---|
| Természetes számok (nem negatív) | 0 ∈ ℕ 0 |
| Egész számok | 0 ∈ ℤ |
| Valós számok | 0 ∈ ℝ |
| Komplex számok | 0 ∈ ℂ |
| Racionális számok | 0 ∈ ℚ |
Nulla páros vagy páratlan szám?
A páros számok halmaza:
{..., -10, -8, -6, -4, -2, 0, 2, 4, 6, 8, 10, ...}
A páratlan számok halmaza:
{..., -9, -7, -5, -3, -1, 1, 3, 5, 7, 9, ...}
A nulla a 2 egész számának többszöröse:
0 × 2 = 0
A Zero a beállított páros számok tagja:
0 ∈ {2 k , k ∈ℤ}
Tehát a nulla páros és nem páratlan szám.
A nulla természetes szám?
A meghatározott természetes számokra két definíció van.
A nem negatív egészek halmaza:
ℕ 0 = {0,1,2,3,4,5,6,7,8, ...}
A pozitív egészek halmaza:
ℕ 1 = {1,2,3,4,5,6,7,8, ...}
A Zero a nem negatív egészek halmazának tagja:
0 ∈ ℕ 0
A nulla nem tagja a pozitív egészek halmazának:
0 ℕ ℕ 1
A nulla egész szám?
A teljes számokra három definíció van:
Az egész számok halmaza:
ℤ = {0,1,2,3,4,5,6,7,8, ...}
A nem negatív egészek halmaza:
ℕ 0 = {0,1,2,3,4,5,6,7,8, ...}
A pozitív egészek halmaza:
ℕ 1 = {1,2,3,4,5,6,7,8, ...}
A Zero tagja az egész számok és a nem negatív egészek halmazának:
0 ∈ ℤ
0 ∈ ℕ 0
A nulla nem tagja a pozitív egészek halmazának:
0 ℕ ℕ 1
A nulla egész szám?
Az egész számok halmaza:
ℤ = {0,1,2,3,4,5,6,7,8, ...}
A Zero az egész számok halmazának tagja:
0 ∈ ℤ
Tehát a nulla egész szám.
A nulla racionális szám?
A racionális szám két egész szám hányadosaként kifejezhető szám:
ℚ = { n / m ; n , m ∈ℤ}
A nulla két egész szám hányadosaként írható.
Például:
0 = 0/3
Tehát a nulla racionális szám.
A nulla pozitív szám?
A pozitív számot nullánál nagyobb számként definiáljuk:
x / 0
Például:
5/ 0
Mivel a nulla nem nagyobb, mint nulla, nem pozitív szám.
A nulla prímszám?
A 0 szám nem prímszám.
A nulla nem pozitív szám, és végtelen számú osztója van.
A legalacsonyabb prímszám 2.