期待値
確率と統計では、期待値または期待値は、確率変数の加重平均値です。
連続確率変数の期待値
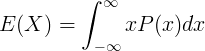
E(X)は、連続確率変数Xの期待値です。
xは、連続確率変数Xの値です。
P(x)は確率密度関数です
離散確率変数の期待値
![]()
E(X)は、連続確率変数Xの期待値です。
xは、連続確率変数Xの値です。
P(x)はXの確率質量関数です
期待値の性質
直線性
aが定数で、X、Yが確率変数の場合:
E(aX)= aE(X)
E(X + Y)= E(X)+ E(Y)
絶え間ない
cが定数の場合:
E(c)= c
製品
XとYが独立確率変数の場合:
E(X⋅Y)= E(X)⋅E (Y)
条件付き期待値