基本的な確率式

確率範囲

0≤ P （ A ）≤1

補足イベントのルール

P （ A ^C）+ P （ A ）= 1

足し算のルール

P（A∪B）= P（A）+ P（B）-P（A∩B）

ばらばらのイベント

イベントAとBは互いに素です。

P（A∩B）= 0

条件付き確率

P（A | B）= P（A∩B）/ P（B）

ベイズフォーミュラ

P（A | B）= P（B | A）・P（A）/ P（B）

独立したイベント

イベントAとBは、独立している場合

P（A∩B）= P（A）・P（B）

累積分布関数

F _X（X）= P（X ≤ X）

確率質量関数

確率密度関数

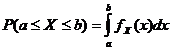
共分散

相関

ベルヌーイ：0-失敗1-成功

幾何学的：0-失敗1-成功

超幾何：K個の成功オブジェクトを持つN個のオブジェクト、n個のオブジェクトが取得されます。