分散

確率と統計では、確率変数の分散は、平均値からの2乗距離の平均値です。これは、確率変数が平均値の近くにどのように分布しているかを表します。分散が小さい場合は、確率変数が平均値の近くに分布していることを示します。大きな分散は、確率変数が平均値から遠く離れて分布していることを示します。たとえば、正規分布では、狭いベル曲線の分散は小さく、広いベル曲線の分散は大きくなります。

分散の定義

確率変数Xの分散は、Xの差の2乗の期待値と期待値μです。

σ 2 =ヴァー（X）= E [（X - μ）2 ]

分散の定義から、次のようになります。

σ 2 =ヴァー（X）= E（X 2） - μ 2

連続確率変数の分散

平均値μと確率密度関数f（x）を持つ連続確率変数の場合：

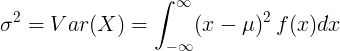
\ sigma ^ 2 = Var（X）= \ int _ {-\ infty} ^ {\ infty}（x- \ mu）^ 2 \：f（x）dx

または

Var（X）= \ left [\ int _ {-\ infty} ^ {\ infty} x ^ 2 \：f（x）dx \ right]-\ mu ^ 2

離散確率変数の分散

平均値μと確率質量関数P（x）を持つ離散確率変数Xの場合：

\ sigma ^ 2 = Var（X）= \ sum_ {i} ^ {}（x_i- \ mu _X）^ 2P_X（x_i）

または

Var（X）= \ left [\ sum_ {i} ^ {} x_i ^ 2P（x_i）\ right]-\ mu ^ 2

分散の特性

XとYが独立確率変数の場合：

Var（X + Y）= Var（X）+ Var（Y）

 

標準偏差►

 

も参照してください

確率と統計
迅速なテーブル