確率分布
確率と統計では、分布は確率変数の特性であり、各値の確率変数の確率を表します。
各分布には、特定の確率密度関数と確率分布関数があります。
確率分布の数は不定ですが、いくつかの一般的な分布が使用されています。
累積分布関数
確率分布は、累積分布関数F(x)によって記述されます。
これは、確率変数Xがx以下の値を取得する確率です。
F(X)= P(X ≤ X)
連続配布
累積分布関数F(x)は、連続確率変数Xの確率密度関数f(u)の積分によって計算されます。
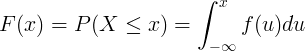
個別配布
累積分布関数F(x)は、離散確率変数Xの確率質量関数P(u)の合計によって計算されます。
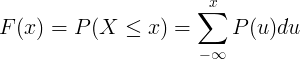
連続分布表
連続分布は、連続確率変数の分布です。
連続分布の例
..。
連続分布表
| ディストリビューション名 | 分布記号 | 確率密度関数(pdf) | 平均 | 分散 |
|---|---|---|---|---|
| f X(x) |
μ = E(X) |
σ 2 =ヴァー(X) |
||
| 正規/ガウス | X〜N(μ、σ 2) |
|
μ | σ 2 |
| ユニフォーム | X〜U(、B) |
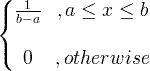 |
|
|
| 指数関数的 | X〜EXP(λ) | |
|
|
| ガンマ | X〜ガンマ(C、λ) | 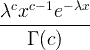 x / 0、c / 0、λ/ 0 |
|
|
| カイ二乗 | X〜 χ 2(K) |
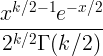 |
k |
2 k |
| ウィシャート | ||||
| F | X〜F(K 1 、K 2) |
|||
| ベータ | ||||
| ワイブル | ||||
| 対数正規 | X〜LN(μ、σ 2) |
|||
| レイリー | ||||
| コーシー | ||||
| ディリクレ | ||||
| ラプラス | ||||
| 徴収 | ||||
| ご飯 | ||||
| スチューデントのt |
離散分布表
離散分布は、離散確率変数の分布です。
離散分布の例
..。
離散分布表
| ディストリビューション名 | 分布記号 | 確率質量関数(pmf) | 平均 | 分散 | |
|---|---|---|---|---|---|
| f x(k)= P(X = k) k = 0,1,2、..。 |
E(x) | VAR(X) | |||
| 二項 | X〜ビン(N、P) |
|
np |
np(1- p) |
|
| ポアソン | X〜ポアソン(λ) |
|
λ≥0 |
λ |
λ |
| ユニフォーム | X〜U(A、B) |
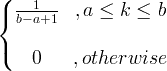 |
|
|
|
| 幾何学的 | X〜はGeom(P) |
|
|
|
|
| 超幾何 | X〜HG(N、K、N) |
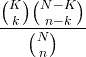 |
N = 0,1,2、..。 K = 0,1、..、N n = 0,1、...、N |
|
|
| ベルヌーイ | X〜ベルン(P) |
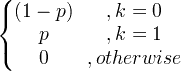 |
p |
p(1- p) |
|