標準偏差

確率と統計では、確率変数の標準偏差は、平均値からの確率変数の平均距離です。

これは、確率変数が平均値の近くにどのように分布しているかを表します。標準偏差が小さいということは、確率変数が平均値の近くに分布していることを示しています。標準偏差が大きいということは、確率変数が平均値から遠く離れて分布していることを示しています。

標準偏差は、確率変数Xの分散の平方根であり、平均値はμです。

$\ sigma = std（X）= \ sqrt {Var（X）} = \ sqrt {E（（X- \ mu）^ 2}$

標準偏差の定義から、次のようになります。

$\ sigma = std（X）= \ sqrt {E（X ^ 2）-\ mu ^ 2}$

平均値μと確率密度関数f（x）を持つ連続確率変数の場合：

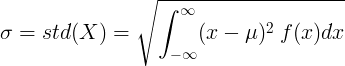
$\ sigma = std（X）= \ sqrt {\ int _ {-\ infty} ^ {\ infty}（x- \ mu）^ 2 \：f（x）dx}$

または

$\ sigma = std（X）= \ sqrt {\ left [\ int _ {-\ infty} ^ {\ infty} x ^ 2 \：f（x）dx \ right]-\ mu ^ 2}$

平均値μと確率質量関数P（x）を持つ離散確率変数Xの場合：

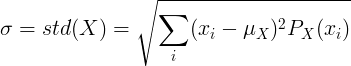
$\ sigma = std（X）= \ sqrt {\ sum_ {i} ^ {}（x_i- \ mu _X）^ 2P_X（x_i）}$

または

$\ sigma = std（X）= \ sqrt {\ left [\ sum_ {i} ^ {} x_i ^ 2P（x_i）\ right]-\ mu ^ 2}$

も参照してください