ಇ ಸ್ಥಿರ

ಇ ಸ್ಥಿರ ಅಥವಾ ಯೂಲರ್ ಸಂಖ್ಯೆ ಗಣಿತದ ಸ್ಥಿರವಾಗಿರುತ್ತದೆ. ಇ ಸ್ಥಿರವು ನೈಜ ಮತ್ತು ಅಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆ.

e = 2.718281828459 ...

ಇ ವ್ಯಾಖ್ಯಾನ
ಇ ಗುಣಲಕ್ಷಣಗಳು
ಮೂಲ ಇ ಲಾಗರಿಥಮ್
ಘಾತೀಯ ಕಾರ್ಯ
ಯೂಲರ್‌ನ ಸೂತ್ರ

ಇ ವ್ಯಾಖ್ಯಾನ

ಇ ಸ್ಥಿರವನ್ನು ಮಿತಿ ಎಂದು ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ:

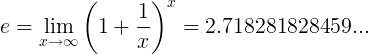
$e = \ lim_ {x \ rightarrow \ infty} \ left (1+ \ frac {1} {x} \ right) ^ x = 2.718281828459 ...$

ಪರ್ಯಾಯ ವ್ಯಾಖ್ಯಾನಗಳು

ಇ ಸ್ಥಿರವನ್ನು ಮಿತಿ ಎಂದು ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ:

$e = \ lim_ {x \ ಬಲಗಡೆ 0} \ ಎಡ (1+ \ ಬಲ x) ^ \ frac {1} {x}$

ಇ ಸ್ಥಿರವನ್ನು ಅನಂತ ಸರಣಿ ಎಂದು ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ:

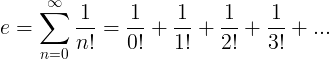
$e = \ sum_ {n = 0} ^ {\ infty} \ frac {1} {n!} = \ frac {1} {0!} + \ frac {1} {1!} + \ frac {1} {. 2!} + \ Frac {1} {3!} + ...$

ಇ ಗುಣಲಕ್ಷಣಗಳು

ಇ ಯ ಪರಸ್ಪರ

ಇ ಯ ಪರಸ್ಪರ ಸಂಬಂಧವು ಮಿತಿಯಾಗಿದೆ:

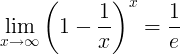
$\ lim_ {x \ rightarrow \ infty} \ left (1- \ frac {1} {x} \ right) ^ x = \ frac {1} {e}$

ಇ ಉತ್ಪನ್ನಗಳು

ಘಾತೀಯ ಕ್ರಿಯೆಯ ವ್ಯುತ್ಪನ್ನವು ಘಾತೀಯ ಕ್ರಿಯೆ:

( e ^x ) '= e ^x

ನೈಸರ್ಗಿಕ ಲಾಗರಿಥಮ್ ಕ್ರಿಯೆಯ ವ್ಯುತ್ಪನ್ನವು ಪರಸ್ಪರ ಕ್ರಿಯೆಯಾಗಿದೆ:

(ಲಾಗ್ _ಇ x ) '= (ಎಲ್ಎನ್ ಎಕ್ಸ್ )' = 1 / ಎಕ್ಸ್

ಇ ಯ ಸಮಗ್ರತೆಗಳು

ಘಾತೀಯ ಕ್ರಿಯೆ e ^x ನ ಅನಿರ್ದಿಷ್ಟ ಅವಿಭಾಜ್ಯವೆಂದರೆ ಘಾತೀಯ ಕ್ರಿಯೆ e ^x .

∫ ಇ ^ಕ್ಷ dx ನ್ನು = ಇ ^{ಎಕ್ಸ್} ಮತ್ತು + c

ನೈಸರ್ಗಿಕ ಲಾಗರಿಥಮ್ ಕಾರ್ಯ ಲಾಗ್ _ಇ x ನ ಅನಿರ್ದಿಷ್ಟ ಅವಿಭಾಜ್ಯ :

Log _e x dx = ∫ ln x dx = x ln x - x + c

1 / x ಪರಸ್ಪರ ಕ್ರಿಯೆಯ 1 ರಿಂದ ಇ ವರೆಗಿನ ನಿರ್ದಿಷ್ಟ ಅವಿಭಾಜ್ಯ 1:

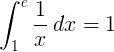
$\ int_ {1} ^ {e} \ frac {1} {x} \: dx = 1$

ಮೂಲ ಇ ಲಾಗರಿಥಮ್

X ಸಂಖ್ಯೆಯ ನೈಸರ್ಗಿಕ ಲಾಗರಿಥಮ್ ಅನ್ನು x ನ ಮೂಲ ಇ ಲಾಗರಿಥಮ್ ಎಂದು ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ:

ln x = ಲಾಗ್ _ಇ x

ಘಾತೀಯ ಕಾರ್ಯ

ಘಾತೀಯ ಕಾರ್ಯವನ್ನು ಹೀಗೆ ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ:

f ( x ) = exp ( x ) = e ^x

ಯೂಲರ್‌ನ ಸೂತ್ರ

ಸಂಕೀರ್ಣ ಸಂಖ್ಯೆ e ^iθ ಗುರುತನ್ನು ಹೊಂದಿದೆ:

ಇ ^iθ = ಕಾಸ್ ( θ ) + ನಾನು ಪಾಪದ ( θ )

ನಾನು ಕಾಲ್ಪನಿಕ ಘಟಕ (-1 ರ ವರ್ಗಮೂಲ).

Any ಯಾವುದೇ ನೈಜ ಸಂಖ್ಯೆ.