ಘಾತಾಂಕ ನಿಯಮಗಳು
ಘಾತೀಯ ನಿಯಮಗಳು, ಘಾತಾಂಕದ ನಿಯಮಗಳು ಮತ್ತು ಉದಾಹರಣೆಗಳು.
ಘಾತಾಂಕ ಎಂದರೇನು
N ನ ಶಕ್ತಿಗೆ ಎತ್ತರಿಸಿದ ಬೇಸ್ a, n ಬಾರಿ ಗುಣಾಕಾರಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ:
a n = a × a × ... × a
n ಬಾರಿ
a ಬೇಸ್ ಮತ್ತು n ಘಾತಾಂಕ.
ಉದಾಹರಣೆಗಳು
3 1 = 3
3 2 = 3 × 3 = 9
3 3 = 3 × 3 × 3 = 27
3 4 = 3 × 3 × 3 × 3 = 81
3 5 = 3 × 3 × 3 × 3 × 3 = 243
ಘಾತಾಂಕ ನಿಯಮಗಳು ಮತ್ತು ಗುಣಲಕ್ಷಣಗಳು
| ನಿಯಮದ ಹೆಸರು | ನಿಯಮ | ಉದಾಹರಣೆ |
|---|---|---|
| ಉತ್ಪನ್ನ ನಿಯಮಗಳು | ಒಂದು ಎನ್ ⋅ ಒಂದು ಮೀ = ಒಂದು n + m ನ | 2 3 ⋅ 2 4 = 2 3 + 4 = 128 |
| ಒಂದು ಎನ್ ⋅ ಬಿ ಎನ್ = ( ಒಂದು ⋅ ಬಿ ) ಎನ್ | 3 2 ⋅ 4 2 = (3⋅4) 2 = 144 | |
| ಪ್ರಮಾಣ ನಿಯಮಗಳು | a n / a m = a n - m | 2 5 /2 3 = 2 5-3 = 4 |
| a n / b n = ( a / b ) n | 4 3 /2 3 = (4/2) 3 = 8 | |
| ವಿದ್ಯುತ್ ನಿಯಮಗಳು | ( b n ) m = b n⋅m | (2 3 ) 2 = 2 3⋅2 = 64 |
| b n m = b ( n m ) | 2 3 2 = 2 ( 3 2 ) = 512 | |
| m ( b n ) = b n / m | 2 (2 6 ) = 2 6/2 = 8 | |
| b 1 / n = n √ b | 8 1/3 = 3 √ 8 = 2 | |
| ನಕಾರಾತ್ಮಕ ಘಾತಾಂಕಗಳು | b -n = 1 / b n | 2 -3 = 1/2 3 = 0.125 |
| ಶೂನ್ಯ ನಿಯಮಗಳು | b 0 = 1 | 5 0 = 1 |
| 0 n = 0, n / 0 ಗೆ | 0 5 = 0 | |
| ಒಂದು ನಿಯಮಗಳು | ಬೌ 1 = ಬಿ | 5 1 = 5 |
| 1 n = 1 | 1 5 = 1 | |
| ಮೈನಸ್ ಒಂದು ನಿಯಮ | 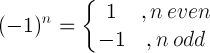 |
(-1) 5 = -1 |
| ವ್ಯುತ್ಪನ್ನ ನಿಯಮ | ( x n ) ' = n ⋅ x n -1 | ( x 3 ) ' = 3⋅ x 3-1 |
| ಸಮಗ್ರ ನಿಯಮ | ∫ ಕ್ಷ ಎನ್ dx ನ್ನು = ಕ್ಷ ಎನ್ +1 ಅನ್ನು / ( ಎನ್ +1) + ಸಿ | ∫ ಕ್ಷ 2 dx ನ್ನು = ಕ್ಷ 2 +1 / (2 +1) + ಸಿ |
ಘಾತಾಂಕ ಉತ್ಪನ್ನ ನಿಯಮಗಳು
ಒಂದೇ ಮೂಲವನ್ನು ಹೊಂದಿರುವ ಉತ್ಪನ್ನ ನಿಯಮ
ಒಂದು ಎನ್ ⋅ ಒಂದು ಮೀ = ಒಂದು n + m ನ
ಉದಾಹರಣೆ:
2 3 2 4 = 2 3 + 4 = 2 7 = 2⋅2⋅2⋅2⋅2⋅2⋅2 = 128
ಅದೇ ಘಾತಾಂಕದೊಂದಿಗೆ ಉತ್ಪನ್ನ ನಿಯಮ
ಒಂದು ಎನ್ ⋅ ಬಿ ಎನ್ = ( ಒಂದು ⋅ ಬಿ ) ಎನ್
ಉದಾಹರಣೆ:
3 2 ⋅ 4 2 = (3⋅4) 2 = 12 2 = 12⋅12 = 144
ನೋಡಿ: ಘಾತಾಂಕಗಳನ್ನು ಗುಣಿಸುವುದು
ಘಾತಾಂಕದ ಅಂಶ ನಿಯಮಗಳು
ಒಂದೇ ಮೂಲವನ್ನು ಹೊಂದಿರುವ ಪ್ರಮಾಣ ನಿಯಮ
a n / a m = a n - m
ಉದಾಹರಣೆ:
2 5 /2 3 = 2 5-3 = 2 2 = 2⋅2 = 4
ಅದೇ ಘಾತಾಂಕದೊಂದಿಗೆ ಪ್ರಮಾಣ ನಿಯಮ
a n / b n = ( a / b ) n
ಉದಾಹರಣೆ:
4 3 /2 3 = (4/2) 3 = 2 3 = 2⋅2⋅2 = 8
ನೋಡಿ: ಘಾತಾಂಕಗಳನ್ನು ವಿಭಜಿಸುವುದು
ಘಾತಾಂಕಗಳು ವಿದ್ಯುತ್ ನಿಯಮಗಳು
ವಿದ್ಯುತ್ ನಿಯಮ I.
( a n ) m = a n⋅m
ಉದಾಹರಣೆ:
(2 3 ) 2 = 2 3⋅2 = 2 6 = 2⋅2⋅2⋅2⋅2⋅2 = 64
ವಿದ್ಯುತ್ ನಿಯಮ II
a n m = a ( n m )
ಉದಾಹರಣೆ:
2 3 2 = 2 (3 2 ) = 2 (3⋅3) = 2 9 = 2⋅2⋅2⋅2⋅2⋅2⋅2⋅2⋅2 = 512
ಆಮೂಲಾಗ್ರಗಳೊಂದಿಗೆ ವಿದ್ಯುತ್ ನಿಯಮ
m √ ( a n ) = a n / m
ಉದಾಹರಣೆ:
2 (2 6 ) = 2 6/2 = 2 3 = 2⋅2⋅2 = 8
Neg ಣಾತ್ಮಕ ಘಾತಾಂಕಗಳ ನಿಯಮ
b -n = 1 / b n
ಉದಾಹರಣೆ:
2 -3 = 1/2 3 = 1 / (2⋅2⋅2) = 1/8 = 0.125
ನೋಡಿ: ನಕಾರಾತ್ಮಕ ಘಾತಾಂಕಗಳು
ಸಹ ನೋಡಿ
- ಘಾತಾಂಕಗಳನ್ನು ಸೇರಿಸಲಾಗುತ್ತಿದೆ
- ಘಾತಾಂಕಗಳನ್ನು ವಿಭಜಿಸುವುದು
- ಭಾಗಶಃ ಘಾತಾಂಕಗಳು
- ಘಾತಾಂಕಗಳನ್ನು ಗುಣಿಸುವುದು
- ನಕಾರಾತ್ಮಕ ಘಾತಾಂಕಗಳು
- ಘಾತಾಂಕಗಳನ್ನು ಸರಳಗೊಳಿಸುವುದು
- ಶೂನ್ಯ ಘಾತಾಂಕ
- ಘಾತಾಂಕ ಕ್ಯಾಲ್ಕುಲೇಟರ್
- ಲಾಗರಿಥಮ್ ಕ್ಯಾಲ್ಕುಲೇಟರ್
- ಘಾತೀಯ ಬೆಳವಣಿಗೆಯ ಕ್ಯಾಲ್ಕುಲೇಟರ್
- ಆಂಟಿಲಾಗ್ ಕ್ಯಾಲ್ಕುಲೇಟರ್
- ಲಾಗ್ (x) ನಿಯಮಗಳು
- ln (x) ನಿಯಮಗಳು
- ಇ ಸ್ಥಿರ