지수 규칙
지수 규칙, 지수 법칙 및 예.
지수는 무엇입니까
n의 거듭 제곱으로 올린 밑수 a는 a의 n 곱하기와 같습니다.
, n은 = × × ... ×
n 번
a는 밑이고 n은 지수입니다.
예
3 1 = 3
3 2 = 3 × 3 = 9
3 3 = 3 × 3 × 3 = 27
(3) (4) = 3 × 3 × 3 × 3 = 81
(3) (5) = 3 × 3 × 3 × 3 × 3 = 243
지수 규칙 및 속성
| 규칙 이름 | 규칙 | 예 |
|---|---|---|
| 제품 규칙 | a n ⋅ a m = a n + m | 2 3 ⋅ 2 4 = 2 3 + 4 = 128 |
| a n ⋅ b n = ( a ⋅ b ) n | 3 2 ⋅ 4 2 = (3⋅4) 2 = 144 | |
| 몫 규칙 | a n / a m = a n - m | 2 5 / 2 (3) = 2 5-3 = 4 |
| a n / b n = ( a / b ) n | 4 (3) / 2 (3) = (4/2) 3 = 8 | |
| 전력 규칙 | ( B의 N ) m = B n⋅m | (2 3 ) 2 = 2 3⋅2 = 64 |
| b n m = b ( n m ) | 2 3 2 = 2 ( 3 2 ) = 512 | |
| m √ ( B 형 N ) = B N / m | 2 √ (2 6 ) = 2 6/2 = 8 | |
| B (1) / N = N √ B | 8 1/3 = 3 √ 8 = 2 | |
| 음의 지수 | B -n = 1 / (B) N | 2 -3 = 1/2 3 = 0.125 |
| 제로 규칙 | b 0 = 1 | 5 0 = 1 |
| 0 n = 0, n / 0 인 경우 | 0 5 = 0 | |
| 하나의 규칙 | b 1 = b | 5 1 = 5 |
| 1 N = 1 | 1 5 = 1 | |
| 마이너스 하나의 규칙 | 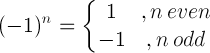 |
(-1) 5 = -1 |
| 미분 규칙 | ( X의 N ) ' = N ⋅ X N -1 | ( x 3 ) ' = 3⋅ x 3-1 |
| 적분 규칙 | ∫ X N DX = X N +1 / ( N + 1) + C | ∫ x 2 dx = x 2 + 1 / (2 + 1) + C |
지수 곱 규칙
기본이 동일한 제품 규칙
a n ⋅ a m = a n + m
예:
2 3 ⋅ 2 4 = 2 3 + 4 = 2 7 = 2⋅2⋅2⋅2⋅2⋅2⋅2 = 128
지수가 동일한 곱 규칙
a n ⋅ b n = ( a ⋅ b ) n
예:
3 2 ⋅ 4 2 = (3⋅4) 2 = 12 2 = 12⋅12 = 144
참조 : 다중 지수
지수 몫 규칙
기본이 같은 몫 규칙
a n / a m = a n - m
예:
2 5 / 2 (3) = 2 5-3 = 2 (2) = 4 = 2⋅2
지수가 같은 몫 규칙
a n / b n = ( a / b ) n
예:
4 (3) / 2 (3) = (4/2) (3) = 2 3 = 8 = 2⋅2⋅2
참조 : 지수 나누기
지수 거듭 제곱 규칙
파워 룰 I
( a n ) m = a n⋅m
예:
(2 3 ) 2 = 2 3⋅2 = 2 6 = 2⋅2⋅2⋅2⋅2⋅2 = 64
파워 룰 II
a n m = a ( n m )
예:
2 3 2 = 2 (3 2 ) = 2 (3⋅3) = 2 9 = 2⋅2⋅2⋅2⋅2⋅2⋅2⋅2⋅2 = 512
급진파가있는 전력 규칙
m √ ( N은 ) = N / m을
예:
2 √ (2 6 ) = 2 6/2 = 2 3 = 2⋅2⋅2 = 8
음의 지수 규칙
B -n = 1 / (B) N
예:
2 -3 = 1/2 3 = 1 / (2⋅2⋅2) = 1/8 = 0.125
참조 : 음의 지수
또한보십시오
- 지수 더하기
- 지수 나누기
- 분수 지수
- 다중 지수
- 음의 지수
- 지수 단순화
- 제로 지수
- 지수 계산기
- 로그 계산기
- 지수 성장 계산기
- Antilog 계산기
- log (x) 규칙
- ln (x) 규칙
- e 상수