Arccos (x) 함수
Arccos (x), cos -1 (x), 역 코사인 함수.
Arccos 정의
x의 아크 코사인은 -1≤x≤1 일 때 x 의 역 코사인 함수 로 정의됩니다 .
y의 코사인이 x와 같을 때 :
cos y = x
그러면 x의 아크 코사인은 y와 같은 x의 역 코사인 함수와 같습니다.
arccos x = cos -1 x = y
(여기서 cos -1 x는 역 코사인을 의미하며 -1의 거듭 제곱에 대한 코사인을 의미하지 않습니다.)
예
arccos 1 = cos -1 1 = 0 rad = 0 °
arccos의 그래프
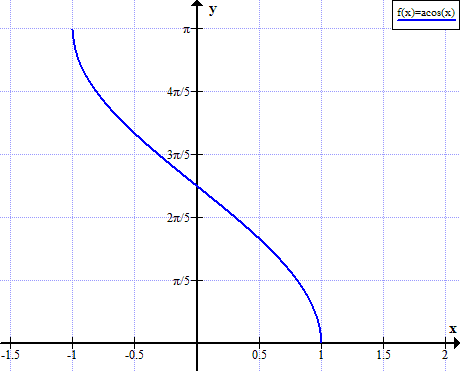
Arccos 규칙
| 규칙 이름 | 규칙 |
|---|---|
| 아크 코사인의 코사인 | cos (arccos x ) = x |
| 코사인의 아크 코사인 | arccos (cos x ) = x + 2 k π, k ∈ℤ ( k 는 정수) |
| 부정적 주장의 Arccos | arccos ( -x ) = π-arccos x = 180 °-arccos x |
| 상보 각 | arccos x = π / 2-arcsin x = 90 °-arcsin x |
| Arccos 합계 | arccos ( α ) + arccos ( β ) = arccos ( αβ - √ (1- α 2 ) (1- β 2 ) ) |
| Arccos 차이 | arccos ( α )-arccos ( β ) = arccos ( αβ + √ (1- α 2 ) (1- β 2 ) ) |
| x의 죄의 아크 코스 | ARCCOS (죄 X ) = - X - (2- K +0.5) π |
| 아크 코사인의 사인 | |
| 아크 코사인의 접선 | 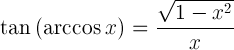 |
| 아크 코사인의 미분 | 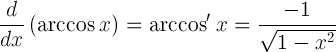 |
| 아크 코사인의 부정적분 | |
Arccos 테이블
| x | arccos (x) (rad) |
arccos (x) (°) |
|---|---|---|
| -1 | π | 180 ° |
| -√ 3 / 2 | 5π / 6 | 150 ° |
| -√ 2 / 2 | 3π / 4 | 135 ° |
| -1/2 | 2π / 3 | 120 ° |
| 0 | π / 2 | 90 ° |
| 1/2 | π / 3 | 60 ° |
| √ 2 / 2 | π / 4 | 45 ° |
| √ 3 / 2 | π / 6 | 30 ° |
| 1 | 0 | 0 ° |
또한보십시오
- 코사인 함수
- 아크 사인 함수
- Arctan 함수
- Arccos 계산기
- 라디안에서도 변환기
- 0의 Arccos
- Arccos of 1
- 2의 Arccos
- 3의 Arccos
- cos의 Arccos
- 죄의 아크 코스
- Arccos 파생 상품
- Arccos 그래프
- arccos의 cos
- Arccos의 죄
- Arccos의 탄