Nulis skaičius (0)
- Nulinio skaičiaus apibrėžimas
- Nulio skaičiaus istorija
- Nulinio skaičiaus savybės
- Rinkiniai, kuriuose yra nulis
Nulinio skaičiaus apibrėžimas
Nulis yra matematikoje naudojamas skaičius, apibūdinantis kiekį ar nulį.
Kai ant stalo yra 2 obuoliai, o mes paimame 2 obuolius, galime sakyti, kad ant stalo yra nulis obuolių.
Nulis skaičius nėra teigiamas skaičius ir nėra neigiamas skaičius.
Nulis taip pat yra vietos ženklo skaitmuo kitais skaičiais (pvz .: 40,103, 170).
Ar nulis yra skaičius?
Nulis yra skaičius. Tai nėra teigiamas ar neigiamas skaičius.
Nulis skaitmuo
Nulis skaitmuo naudojamas kaip vietos rezervavimo priemonė rašant skaičius.
Pavyzdžiui:
204 = 2 × 100 + 0 × 10 + 4 × 1
Nulio skaičiaus istorija
Kas išrado nulinį skaičių?
Šiuolaikinis simbolis 0 buvo išrastas Indijoje VI a., Vėliau jį naudojo persai ir arabai, o vėliau ir Europoje.
Nulio simbolis
Nulis skaičius žymimas simboliu 0 .
Arabų skaitmenų sistemoje naudojamas simbolis ٠.
Nulinio skaičiaus savybės
x reiškia bet kurį skaičių.
| Operacija | Taisyklė | Pavyzdys |
|---|---|---|
Papildymas |
x + 0 = x |
3 + 0 = 3 |
Atimtis |
x - 0 = x |
3 - 0 = 3 |
Dauginimas |
x × 0 = 0 |
5 × 0 = 0 |
Skyrius |
0 ÷ x = 0 , kai x ≠ 0 |
0 ÷ 5 = 0 |
| x ÷ 0 nėra apibrėžtas |
5 ÷ 0 nėra apibrėžtas |
|
Išskleidimas |
0 x = 0 |
0 5 = 0 |
| x 0 = 1 |
5 0 = 1 |
|
Šaknis |
√ 0 = 0 |
|
Logaritmas |
log b (0) nėra apibrėžtas |
|
| |
||
Faktoralis |
0! = 1 |
|
Sinusas |
nuodėmė 0º = 0 |
|
Kosinusas |
cos 0 ° = 1 |
|
Tangentas |
įdegis 0º = 0 |
|
Išvestinė |
0 '= 0 |
|
Integralus |
∫ 0 d x = 0 + C |
|
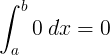 |
Nulis be to
Skaičiaus plius nulis pridėjimas yra lygus skaičiui:
x + 0 = x
Pavyzdžiui:
5 + 0 = 5
Nulis atimtis
Skaičiaus, atėmus nulį, atėmimas yra lygus skaičiui:
x - 0 = x
Pavyzdžiui:
5 - 0 = 5
Padauginta iš nulio
Skaičiaus, padauginto iš nulio, padauginimas yra lygus nuliui:
x × 0 = 0
Pavyzdžiui:
5 × 0 = 0
Skaičius padalytas iš nulio
Skaičiaus padalijimas iš nulio nėra apibrėžtas:
x ÷ 0 nėra apibrėžtas
Pavyzdžiui:
5 ÷ 0 nėra apibrėžtas
Nulis padalintas iš skaičiaus
Nulio padalijimas iš skaičiaus yra nulis:
0 ÷ x = 0
Pavyzdžiui:
0 ÷ 5 = 0
Skaičius iki nulio galios
Nulio pakelto skaičiaus galia yra viena:
x 0 = 1
Pavyzdžiui:
5 0 = 1
Nulio logaritmas
B nulinis nulinis logaritmas nėra apibrėžtas:
log b (0) nėra apibrėžtas
Nėra skaičiaus, kuriuo galėtume pakelti bazę b, kad gautume nulį.
Tik bazinio b logaritmo x riba, kai x konverguoja nulį, yra minus begalybė:
![]()
Rinkiniai, kuriuose yra nulis
Nulis yra natūralių skaičių, sveikųjų skaičių, tikrųjų skaičių ir kompleksinių skaičių rinkinių elementas:
| Nustatyti | Nustatykite narystės žymėjimą |
|---|---|
| Natūralūs skaičiai (ne neigiami) | 0 ∈ ℕ 0 |
| Sveikas skaičius | 0 ∈ ℤ |
| Tikrieji skaičiai | 0 ∈ ℝ |
| Sudėtingi skaičiai | 0 ∈ ℂ |
| Racionalūs numeriai | 0 ∈ ℚ |
Ar nulis yra lyginis ar nelyginis skaičius?
Lyginių skaičių rinkinys yra:
{..., -10, -8, -6, -4, -2, 0, 2, 4, 6, 8, 10, ...}
Nelyginių skaičių rinkinys yra:
{..., -9, -7, -5, -3, -1, 1, 3, 5, 7, 9, ...}
Nulis yra sveikasis skaičius, kartojamas iš 2:
0 × 2 = 0
Nulis yra nustatytų lyginių skaičių narys:
0 ∈ {2 k , k ∈ℤ}
Taigi nulis yra lyginis skaičius, o ne nelyginis skaičius.
Ar nulis yra natūralus skaičius?
Yra du nustatytų natūraliųjų skaičių apibrėžimai.
Ne neigiamų sveikųjų skaičių rinkinys:
ℕ 0 = {0,1,2,3,4,5,6,7,8, ...}
Teigiamų sveikųjų skaičių rinkinys:
ℕ 1 = {1,2,3,4,5,6,7,8, ...}
Nulis yra ne neigiamų sveikųjų skaičių rinkinio narys:
0 ∈ ℕ 0
Nulis nėra teigiamų sveikųjų skaičių rinkinio narys:
0 ∉ ℕ 1
Ar nulis yra sveikas skaičius?
Yra trys sveikųjų skaičių apibrėžimai:
Sveikųjų skaičių rinkinys:
ℤ = {0,1,2,3,4,5,6,7,8, ...}
Ne neigiamų sveikųjų skaičių rinkinys:
ℕ 0 = {0,1,2,3,4,5,6,7,8, ...}
Teigiamų sveikųjų skaičių rinkinys:
ℕ 1 = {1,2,3,4,5,6,7,8, ...}
Nulis yra sveikųjų skaičių ir ne neigiamų sveikųjų skaičių rinkinio narys:
0 ∈ ℤ
0 ∈ ℕ 0
Nulis nėra teigiamų sveikųjų skaičių rinkinio narys:
0 ∉ ℕ 1
Ar nulis yra sveikas skaičius?
Sveikųjų skaičių rinkinys:
ℤ = {0,1,2,3,4,5,6,7,8, ...}
Nulis yra sveikųjų skaičių rinkinio narys:
0 ∈ ℤ
Taigi nulis yra sveikasis skaičius.
Ar nulis yra racionalus skaičius?
Racionalus skaičius yra skaičius, kurį galima išreikšti dviejų sveikųjų skaičių dalimi:
ℚ = { n / m ; n , m ∈ℤ}
Nulis gali būti parašytas kaip dviejų sveikųjų skaičių dalmuo.
Pavyzdžiui:
0 = 0/3
Taigi nulis yra racionalus skaičius.
Ar nulis yra teigiamas skaičius?
Teigiamas skaičius apibrėžiamas kaip skaičius, didesnis nei nulis:
x / 0
Pavyzdžiui:
5/ 0
Kadangi nulis nėra didesnis už nulį, tai nėra teigiamas skaičius.
Ar nulis yra pagrindinis skaičius?
Skaičius 0 nėra pirminis skaičius.
Nulis nėra teigiamas skaičius ir turi begalinį daliklių skaičių.
Mažiausias pirminis skaičius yra 2.