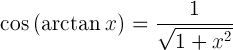Arktangentā funkcija
Arktāns (x), iedegums -1 (x), apgrieztā pieskares funkcija.
Arktāna definīcija
X arktangents ir definēts kā x apgrieztā tangenta funkcija, kad x ir reāls (x ∈ℝ ).
Kad y tangenss ir vienāds ar x:
iedegums y = x
Tad x arktangents ir vienāds ar x apgriezto pieskares funkciju, kas ir vienāda ar y:
arktāns x = tan -1 x = y
Piemērs
arktāns 1 = iedegums -1 1 = π / 4 rad = 45 °
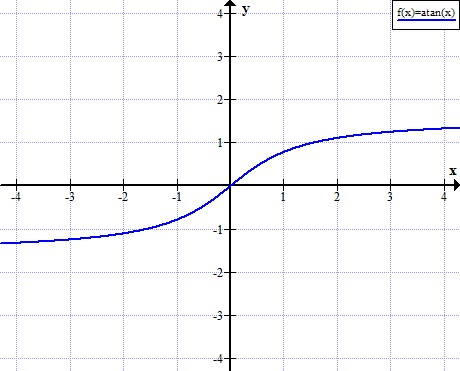
Arktāna grafiks
Arktāna noteikumi
| Kārtulas nosaukums | Noteikums |
|---|---|
| Arkangentes tangents | iedegums (arctan x ) = x |
| Negatīvā argumenta arktāns | arktāns (- x ) = - arktāns x |
| Arktāna summa | arktāns α + arktāns β = arktāns [( α + β ) / (1- αβ )] |
| Arktāna atšķirība | arktāns α - arktāns β = arktāns [( α - β ) / (1+ αβ )] |
| Arktangentā sinusa | |
| Arktangenta kosinuss | |
| Abpusējs arguments |  |
| Arktāns no arcsīna | |
| Arktāna atvasinājums | |
| Nenoteikts arktāna neatņemams elements | |
Arktāna galds
| x | arktāns (x) (rad) |
arktāns (x) (°) |
|---|---|---|
| -∞ | -π / 2 | -90 ° |
| -3 | -1,2490 | -71,565 ° |
| -2 | -1.1071 | -63,435 ° |
| -√ 3 | -π / 3 | -60 ° |
| -1 | -π / 4 | -45 ° |
| -1 / √ 3 | -π / 6 | -30 ° |
| -0,5 | -0,4636 | -26,565 ° |
| 0 | 0 | 0 ° |
| 0.5 | 0,4636 | 26,565 ° |
| 1 / √ 3 | π / 6 | 30 ° |
| 1 | π / 4 | 45 ° |
| √ 3 | π / 3 | 60 ° |
| 2 | 1.1071 | 63,435 ° |
| 3 | 1.2490 | 71,565 ° |
| ∞ | π / 2 | 90 ° |
Skatīt arī
- Tangenta funkcija
- Arkozīna funkcija
- Arcsine funkcija
- Arktāns no 0
- Arktāns no 1
- Arktāns no 2
- Bezgalības arktāns
- Arktāna atvasinājums
- Arktāna neatņemama sastāvdaļa
- Arktāna sine
- Arktāna kosinuss
- Arktāna grafiks
- Arctan kalkulators
- Grādi uz radiāniem pārveidotājs
TRIGONOMETRIJA
- Arccos funkcija
- Arcsin funkcija
- Arktāna funkcija
- Kosinusa funkcija
- Sinusa funkcija
- Tangenta funkcija
ĀTRAS TABULAS