Arccos (x) funkcija
Arccos (x), cos -1 (x), apgrieztā kosinusa funkcija.
Arccos definīcija
Arkazosīns x ir definēts kā x apgrieztā kosinusa funkcija, kad -1≤x≤1.
Kad y kosinuss ir vienāds ar x:
cos y = x
Tad arkazosīns x ir vienāds ar x apgriezto kosinusa funkciju, kas ir vienāds ar y:
arccos x = cos -1 x = y
(Šeit cos -1 x nozīmē apgriezto kosinusu un nenozīmē kosinusu -1 spēkam).
Piemērs
arccos 1 = cos -1 1 = 0 rad = 0 °
Arccos grafiks
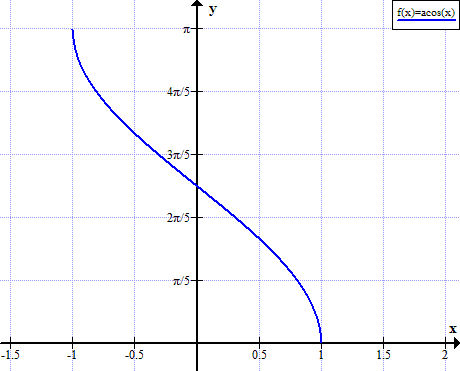
Arccos noteikumi
| Kārtulas nosaukums | Noteikums |
|---|---|
| Arkosīna kosinuss | cos (arccos x ) = x |
| Kosinusa arkozīns | arccos (cos x ) = x + 2 k π, kad k ∈ℤ ( k ir vesels skaitlis) |
| Negatīvs arguments | arccos (- x ) = π - arccos x = 180 ° - arccos x |
| Papildu leņķi | arccos x = π / 2 - arcsin x = 90 ° - arcsin x |
| Arccos summa | arccos ( α ) + arccos ( β ) = arccos ( αβ - √ (1- α 2 ) (1- β 2 ) ) |
| Arccos atšķirība | arccos ( α ) - arccos ( β ) = arccos ( αβ + √ (1- α 2 ) (1- β 2 ) ) |
| X grēka arko | arccos (sin x ) = - x - (2 k +0,5) π |
| Arkozīna sine | |
| Arkozīna tangenss | 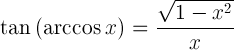 |
| Arkozīna atvasinājums | 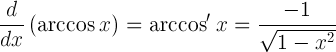 |
| Nenoteikts arkodozīna neatņemamais elements | |
Arccos galds
| x | arccos (x) (rad) |
arccos (x) (°) |
|---|---|---|
| -1 | π | 180 ° |
| -√ 3 /2 | 5π / 6 | 150 ° |
| -√ 2 /2 | 3π / 4 | 135 ° |
| -1/2 | 2π / 3 | 120 ° |
| 0 | π / 2 | 90 ° |
| 1/2 | π / 3 | 60 ° |
| √ 2 /2 | π / 4 | 45 ° |
| √ 3 /2 | π / 6 | 30 ° |
| 1 | 0 | 0 ° |
Skatīt arī
- Kosinusa funkcija
- Arcsine funkcija
- Arktanfunkcija
- Arccos kalkulators
- Radiāni uz grādu pārveidotāju
- 0 Arccos
- 1 Arccos
- 2 Arccos
- 3 Arccos
- Arccos of cos
- Grēka Arko
- Arccos atvasinājums
- Arccos grafiks
- Cos arccos
- Arccos grēks
- Arkaudu iedegums
TRIGONOMETRIJA
- Arccos funkcija
- Arcsin funkcija
- Arktāna funkcija
- Kosinusa funkcija
- Sinusa funkcija
- Tangenta funkcija