ആർക്ക്സൈൻ പ്രവർത്തനം
arcsin (x), sin -1 (x), വിപരീത സൈൻ പ്രവർത്തനം.
ആർക്ക്സിൻ നിർവചനം
X- ന്റെ ആർക്സൈൻ -1≤x≤1 ആയിരിക്കുമ്പോൾ x- ന്റെ വിപരീത സൈൻ ഫംഗ്ഷനായി നിർവചിക്കപ്പെടുന്നു .
Y ന്റെ സൈന് x ന് തുല്യമാകുമ്പോൾ:
sin y = x
X- ന്റെ ആർക്ക്സൈൻ x- ന്റെ വിപരീത സൈൻ ഫംഗ്ഷന് തുല്യമാണ്, അത് y- ന് തുല്യമാണ്:
arcsin x = sin -1 x = y
ഉദാഹരണം
arcsin 1 = sin -1 1 = π / 2 rad = 90 °
ആർക്ക്സിൻ ഗ്രാഫ്
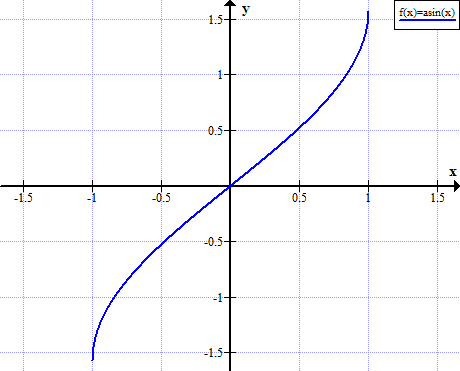
ആർക്ക്സിൻ നിയമങ്ങൾ
| റൂളിന്റെ പേര് | ഭരണം |
|---|---|
| ആർക്ക്സൈനിന്റെ സൈൻ | sin (arcsin x ) = x |
| സൈനിന്റെ ആർക്ക്സൈൻ | arcsin (sin x ) = x +2 k π, k when ( k പൂർണ്ണസംഖ്യയാണെങ്കിൽ) |
| നെഗറ്റീവ് ആർഗ്യുമെന്റിന്റെ ആർക്ക്സിൻ | arcsin (- x ) = - arcsin x |
| കോംപ്ലിമെന്ററി കോണുകൾ | arcsin x = π / 2 - arccos x = 90 ° - arccos x |
| ആർക്ക്സിൻ തുക | arcsin α + arcsin ( β ) = arcsin ( α√ (1- β 2 ) + β√ (1- α 2 ) ) |
| ആർക്ക്സിൻ വ്യത്യാസം | arcsin α - arcsin ( β ) = arcsin ( α√ (1- β 2 ) - β√ (1- α 2 ) ) |
| ആർക്സൈനിന്റെ കോസൈൻ | |
| ആർക്സൈനിന്റെ ടാൻജെന്റ് | |
| ആർക്സൈനിന്റെ ഡെറിവേറ്റീവ് | 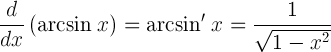 |
| ആർക്സൈനിന്റെ അനിശ്ചിതകാല സംയോജനം |
ആർക്ക്സിൻ പട്ടിക
| x | arcsin (x) (റാഡ്) |
arcsin (x) (°) |
|---|---|---|
| -1 | -π / 2 | -90 ° |
| -√ 3 /2 | -π / 3 | -60 ° |
| -√ 2 /2 | -π / 4 | -45 ° |
| -1/2 | -π / 6 | -30 ° |
| 0 | 0 | 0 ° |
| 1/2 | / 6 | 30 ° |
| √ 2 /2 | / 4 | 45 ° |
| √ 3 /2 | / 3 | 60 ° |
| 1 | / 2 | 90 ° |
ഇതും കാണുക
- സൈൻ പ്രവർത്തനം
- ആർക്കോസിൻ പ്രവർത്തനം
- ആർക്ടാൻ പ്രവർത്തനം
- ആർക്ക്സിൻ കാൽക്കുലേറ്റർ
- റേഡിയൻസ് കൺവെർട്ടറിലേക്കുള്ള ഡിഗ്രികൾ
- 0 ന്റെ ആർക്ക്സിൻ
- 1 ന്റെ ആർക്ക്സിൻ
- അനന്തതയുടെ ആർക്ക്സിൻ
- ആർക്ക്സിൻ ഗ്രാഫ്
- ആർക്സിൻ ഡെറിവേറ്റീവ്
- ആർക്ക്സിൻ ഇന്റഗ്രൽ
- ആർക്ക്സിൻ പാപം
- ആർസ്സിൻ കോസ്
- ആർക്ക്സിൻ ടാൻ