e constante
De constante of het getal van Euler is een wiskundige constante. De constante e is een reëel en irrationeel getal.
e = 2,718281828459 ...
Definitie van e
De constante e wordt gedefinieerd als de limiet:
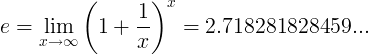
Alternatieve definities
De constante e wordt gedefinieerd als de limiet:
![]()
De constante e wordt gedefinieerd als de oneindige reeks:
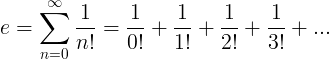
Eigenschappen van e
Wederzijdse van e
Het omgekeerde van e is de limiet:
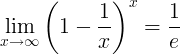
Derivaten van e
De afgeleide van de exponentiële functie is de exponentiële functie:
( e x ) '= e x
De afgeleide van de natuurlijke logaritmefunctie is de wederkerige functie:
(logboek e x ) '= (ln x )' = 1 / x
Integralen van e
De onbepaalde integraal van de exponentiële functie e x is de exponentiële functie e x .
∫ e X dx = e X + c
De onbepaalde integraal van de natuurlijke logaritmefunctie log e x is:
∫ logboek e x dx = ∫ ln x dx = x ln X - X + c
De bepaalde integraal van 1 tot e van de reciproque functie 1 / x is 1:
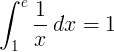
Logaritme met grondtal e
De natuurlijke logaritme van een getal x wordt gedefinieerd als de logaritme met grondtal e van x:
ln x = log e x
Exponentiële functie
De exponentiële functie wordt gedefinieerd als:
f ( x ) = exp ( x ) = e x
Euler's formule
Het complexe getal e iθ heeft de identiteit:
e ik = cos ( θ ) + ik zonde ( θ )
i is de denkbeeldige eenheid (de vierkantswortel van -1).
θ is een reëel getal.
Zie ook
- Hoe e is 2.71828183?
- Logaritme regels
- Natuurlijke logaritme
- Regels voor exponenten
- Normale verdeling
- Pi constant
- e constante - wikipedia