Exponent regels
Exponentregels, exponentwetten en voorbeelden.
Wat is een exponent
De basis a verheven tot de macht van n is gelijk aan de vermenigvuldiging van a, n maal:
een n = a × a × ... × a
n keer
a is de basis en n is de exponent.
Voorbeelden
3 1 = 3
3 2 = 3 × 3 = 9
3 3 = 3 × 3 × 3 = 27
3 4 = 3 × 3 × 3 × 3 = 81
3 5 = 3 × 3 × 3 × 3 × 3 = 243
Exponenten regels en eigenschappen
| Regelnaam | Regel | Voorbeeld |
|---|---|---|
| Product regels | een n ⋅ een m = een n + m | 2 3 ⋅ 2 4 = 2 3 + 4 = 128 |
| een n ⋅ b n = ( een ⋅ b ) n | 3 2 ⋅ 4 2 = (3⋅4) 2 = 144 | |
| Quotiënt regels | a n / a m = a n - m | 2 5 /2 3 = 2 5-3 = 4 |
| een n / b n = ( a / b ) n | 4 3 /2 3 = (4/2) 3 = 8 | |
| Machtsregels | ( b n ) m = b n⋅m | (2 3 ) 2 = 2 3⋅2 = 64 |
| b n m = b ( n m ) | 2 3 2 = 2 ( 3 2 ) = 512 | |
| m √ ( b n ) = b n / m | 2 √ (2 6 ) = 2 6/2 = 8 | |
| b 1 / n = n √ b | 8 1/3 = 3 √ 8 = 2 | |
| Negatieve exponenten | b -n = 1 / b n | 2 -3 = 1/2 3 = 0,125 |
| Geen regels | b 0 = 1 | 5 0 = 1 |
| 0 n = 0, voor n / 0 | 0 5 = 0 | |
| Een regels | b 1 = b | 5 1 = 5 |
| 1 n = 1 | 1 5 = 1 | |
| Minus één regel | 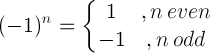 |
(-1) 5 = -1 |
| Afgeleide regel | ( X n ) ' = n ⋅ X n -1 | ( x 3 ) ' = 3⋅ x 3-1 |
| Integrale regel | ∫ X n dx = X n +1 / ( n +1) + C | ∫ X 2 dx = X 2 + 1 / (2 + 1) + C |
Exponenten productregels
Productregel met dezelfde basis
een n ⋅ een m = een n + m
Voorbeeld:
2 3 ⋅ 2 4 = 2 3 + 4 = 2 7 = 2⋅2⋅2⋅2⋅2⋅2⋅2 = 128
Productregel met dezelfde exponent
een n ⋅ b n = ( een ⋅ b ) n
Voorbeeld:
3 2 ⋅ 4 2 = (3⋅4) 2 = 12 2 = 12⋅12 = 144
Zie: Meerdere exponenten
Exponenten quotiëntregels
Quotiëntregel met dezelfde basis
a n / a m = a n - m
Voorbeeld:
2 5 /2 3 = 2 5-3 = 2 2 = 4 = 2⋅2
Quotiëntregel met dezelfde exponent
een n / b n = ( a / b ) n
Voorbeeld:
4 3 /2 3 = (4/2) 3 = 2 3 = 8 = 2⋅2⋅2
Zie: Exponenten delen
Machtsregels voor exponenten
Machtsregel I
( een n ) m = een n⋅m
Voorbeeld:
(2 3 ) 2 = 2 3⋅2 = 2 6 = 2⋅2⋅2⋅2⋅2⋅2 = 64
Machtsregel II
een n m = een ( n m )
Voorbeeld:
2 3 2 = 2 (3 2 ) = 2 (3⋅3) = 2 9 = 2⋅2⋅2⋅2⋅2⋅2⋅2⋅2⋅2 = 512
Machtsregering met radicalen
m √ ( een n ) = een n / m
Voorbeeld:
2 √ (2 6 ) = 2 6/2 = 2 3 = 2⋅2⋅2 = 8
Negatieve exponenten zijn regel
b -n = 1 / b n
Voorbeeld:
2 -3 = 1/2 3 = 1 / (2⋅2⋅2) = 1/8 = 0,125
Zie: Negatieve exponenten
Zie ook
- Exponenten toevoegen
- Exponenten delen
- Fractionele exponenten
- Meerdere exponenten
- Negatieve exponenten
- Exponenten vereenvoudigen
- Nul exponent
- Exponent-rekenmachine
- Logaritme rekenmachine
- Exponentiële groei calculator
- Antilog rekenmachine
- log (x) regels
- ln (x) regels
- e constante