Função Arccos (x)
Arccos (x), cos -1 (x), função cosseno inversa .
Definição de Arccos
O arco cosseno de x é definido como a função cosseno inversa de x quando -1≤x≤1.
Quando o cosseno de y é igual a x:
cos y = x
Então, o arco cosseno de x é igual à função cosseno inversa de x, que é igual a y:
arccos x = cos -1 x = y
(Aqui cos -1 x significa o cosseno inverso e não significa cosseno à potência de -1).
Exemplo
arccos 1 = cos -1 1 = 0 rad = 0 °
Gráfico de arccos
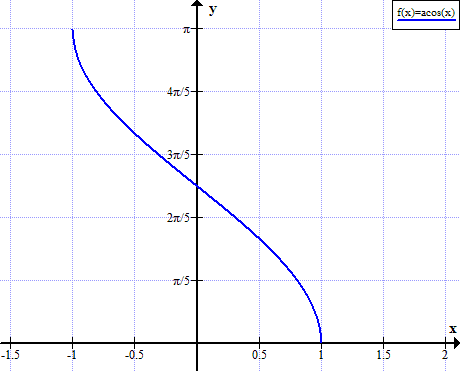
Regras Arccos
| Nome da regra | Regra |
|---|---|
| Cosseno de arco cosseno | cos (arccos x ) = x |
| Arco-cosseno de cosseno | arccos (cos x ) = x + 2 k π, quando k ∈ℤ ( k é inteiro) |
| Arccos de argumento negativo | arccos (- x ) = π - arccos x = 180 ° - arccos x |
| Ângulos complementares | arccos x = π / 2 - arco seno x = 90 ° - arco seno x |
| Soma de Arccos | arccos ( α ) + arccos ( β ) = arccos ( αβ - √ (1- α 2 ) (1- β 2 ) ) |
| Diferença de Arccos | arccos ( α ) - arccos ( β ) = arccos ( αβ + √ (1- α 2 ) (1- β 2 ) ) |
| Arccos do pecado de x | arccos (sin x ) = - x - (2 k +0,5) π |
| Seno de arco cosseno | |
| Tangente de arco cosseno | 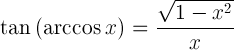 |
| Derivado de arco cosseno | 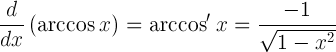 |
| Integral indefinido do arco-cosseno | |
Mesa Arccos
| x | arccos (x) (rad) |
arccos (x) (°) |
|---|---|---|
| -1 | π | 180 ° |
| -√ 3 /2 | 5π / 6 | 150 ° |
| -√ 2 /2 | 3π / 4 | 135 ° |
| -1/2 | 2π / 3 | 120 ° |
| 0 | π / 2 | 90 ° |
| 1/2 | π / 3 | 60 ° |
| √ 2 /2 | π / 4 | 45 ° |
| √ 3 /2 | π / 6 | 30 ° |
| 1 | 0 | 0 ° |
Veja também
- Função cosseno
- Função Arcsine
- Função Arctan
- Calculadora arccos
- Conversor de radianos para graus
- Arccos de 0
- Arccos de 1
- Arccos de 2
- Arccos de 3
- Arccos de cos
- Arccos do pecado
- Derivado de Arccos
- Gráfico Arccos
- Cos of Arccos
- Pecado de arccos
- Bronzeado de arccos