e constantă

E constantă sau numărul lui Euler este o constantă matematică. Constanta e este numărul real și irațional.

e = 2.718281828459 ...

Definiția e
Proprietățile e
Logaritm de bază
Functie exponentiala
Formula lui Euler

Definiția e

Constanta e este definită ca limită:

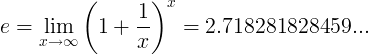
$e = \ lim_ {x \ rightarrow \ infty} \ left (1+ \ frac {1} {x} \ right) ^ x = 2.718281828459 ...$

Definiții alternative

Constanta e este definită ca limită:

$e = \ lim_ {x \ rightarrow 0} \ left (1+ \ right x) ^ \ frac {1} {x}$

Constanta e este definită ca seria infinită:

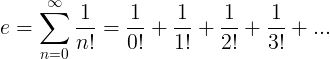
$e = \ sum_ {n = 0} ^ {\ infty} \ frac {1} {n!} = \ frac {1} {0!} + \ frac {1} {1!} + \ frac {1} { 2!} + \ Frac {1} {3!} + ...$

Proprietățile e

Reciprocul e

Reciprocul lui e este limita:

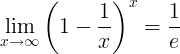
$\ lim_ {x \ rightarrow \ infty} \ left (1- \ frac {1} {x} \ right) ^ x = \ frac {1} {e}$

Derivate ale e

Derivata funcției exponențiale este funcția exponențială:

( e ^x ) '= e ^x

Derivata funcției logaritme naturale este funcția reciprocă:

(log _e x ) '= (ln x )' = 1 / x

Integrale ale e

Integrala nedefinită a funcției exponențiale e ^x este funcția exponențială e ^x .

∫ e ^x dx = e ^x + c

Integrala nedefinită a funcției logaritme naturale log _e x este:

∫ log _e x dx = ∫ ln x dx = x ln x - x + c

Integrala definită de la 1 la e a funcției reciproce 1 / x este 1:

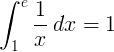
$\ int_ {1} ^ {e} \ frac {1} {x} \: dx = 1$

Logaritm de bază

Logaritmul natural al unui număr x este definit ca baza e logaritmul lui x:

ln x = log _e x

Functie exponentiala

Funcția exponențială este definită ca:

f ( x ) = exp ( x ) = e ^x

Formula lui Euler

Numărul complex e ^iθ are identitatea:

e ^iθ = cos ( θ ) + i sin ( θ )

i este unitatea imaginară (rădăcina pătrată a -1).

θ este orice număr real.