Număr zero (0)
Definiția numărului zero
Zero este un număr utilizat în matematică pentru a descrie cantitatea sau cantitatea nulă.
Când sunt 2 mere pe masă și luăm cele 2 mere, putem spune că sunt zero mere pe masă.
Numărul zero nu este un număr pozitiv și nu un număr negativ.
De asemenea, zero este o cifră de substituent în alte numere (de exemplu: 40.103, 170).
Este zero un număr?
Zero este un număr. Nu este un număr pozitiv și nici negativ.
Cifră zero
Cifra zero este utilizată ca substituent la scrierea numerelor.
De exemplu:
204 = 2 × 100 + 0 × 10 + 4 × 1
Istoricul numărului zero
Cine a inventat numărul zero?
Simbolul modern 0 a fost inventat în India în secolul al VI-lea, folosit mai târziu de persani și arabi și mai târziu în Europa.
Simbolul zero
Numărul zero este notat cu simbolul 0 .
Sistemul cu cifre arabe folosește simbolul ٠.
Proprietăți cu număr zero
x reprezintă orice număr.
| Operațiune | Regulă | Exemplu |
|---|---|---|
Plus |
x + 0 = x |
3 + 0 = 3 |
Scădere |
x - 0 = x |
3 - 0 = 3 |
Multiplicare |
x × 0 = 0 |
5 × 0 = 0 |
Divizia |
0 ÷ x = 0 , când x ≠ 0 |
0 ÷ 5 = 0 |
| x ÷ 0 este nedefinit |
5 ÷ 0 este nedefinit |
|
Exponențierea |
0 x = 0 |
0 5 = 0 |
| x 0 = 1 |
5 0 = 1 |
|
Rădăcină |
√ 0 = 0 |
|
Logaritm |
jurnalul b (0) este nedefinit |
|
| |
||
Factorială |
0! = 1 |
|
Sinus |
sin 0º = 0 |
|
Cosinus |
cos 0º = 1 |
|
Tangentă |
tan 0º = 0 |
|
Derivat |
0 '= 0 |
|
Integral |
∫ 0 d x = 0 + C |
|
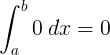 |
Adăugare zero
Adunarea unui număr plus zero este egală cu numărul:
x + 0 = x
De exemplu:
5 + 0 = 5
Scădere zero
Scăderea unui număr minus zero este egală cu numărul:
x - 0 = x
De exemplu:
5 - 0 = 5
Înmulțirea cu zero
Înmulțirea unui număr ori zero este egală cu zero:
x × 0 = 0
De exemplu:
5 × 0 = 0
Număr împărțit la zero
Împărțirea unui număr la zero nu este definită:
x ÷ 0 este nedefinit
De exemplu:
5 ÷ 0 este nedefinit
Zero împărțit la un număr
Împărțirea unui zero cu un număr este zero:
0 ÷ x = 0
De exemplu:
0 ÷ 5 = 0
Număr la puterea zero
Puterea unui număr crescut cu zero este una:
x 0 = 1
De exemplu:
5 0 = 1
Logaritmul zero
Logaritmul de bază b al zero este nedefinit:
jurnalul b (0) este nedefinit
Nu există un număr cu care să putem ridica baza b pentru a obține zero.
Doar limita logaritmului de bază b al lui x, când x converge zero este minus infinit:
![]()
Seturi care conțin zero
Zero este un element al seturilor de numere naturale, numere întregi, numere reale și numere complexe:
| Set | Setați notația de membru |
|---|---|
| Numere naturale (non negative) | 0 ∈ ℕ 0 |
| Numere întregi | 0 ∈ ℤ |
| Numere reale | 0 ∈ ℝ |
| Numere complexe | 0 ∈ ℂ |
| Numere rationale | 0 ∈ ℚ |
Este zero numărul par sau impar?
Setul de numere pare este:
{..., -10, -8, -6, -4, -2, 0, 2, 4, 6, 8, 10, ...}
Setul de numere impare este:
{..., -9, -7, -5, -3, -1, 1, 3, 5, 7, 9, ...}
Zero este un multiplu întreg de 2:
0 × 2 = 0
Zero este un membru al setului de numere pare:
0 ∈ {2 k , k ∈ℤ}
Deci zero este un număr par și nu un număr impar.
Este zero un număr natural?
Există două definiții pentru setul de numere naturale.
Setul de numere întregi non negative:
ℕ 0 = {0,1,2,3,4,5,6,7,8, ...}
Setul de numere întregi pozitive:
ℕ 1 = {1,2,3,4,5,6,7,8, ...}
Zero este un membru al setului de numere întregi care nu sunt negative:
0 ∈ ℕ 0
Zero nu este membru al setului de numere întregi pozitive:
0 ∉ ℕ 1
Este zero un număr întreg?
Există trei definiții pentru numerele întregi:
Setul de numere întregi:
ℤ = {0,1,2,3,4,5,6,7,8, ...}
Setul de numere întregi non negative:
ℕ 0 = {0,1,2,3,4,5,6,7,8, ...}
Setul de numere întregi pozitive:
ℕ 1 = {1,2,3,4,5,6,7,8, ...}
Zero este un membru al setului de numere întregi și al setului de numere întregi care nu sunt negative:
0 ∈ ℤ
0 ∈ ℕ 0
Zero nu este membru al setului de numere întregi pozitive:
0 ∉ ℕ 1
Este zero un număr întreg?
Setul de numere întregi:
ℤ = {0,1,2,3,4,5,6,7,8, ...}
Zero este un membru al setului de numere întregi:
0 ∈ ℤ
Deci zero este un număr întreg.
Este zero un număr rațional?
Un număr rațional este un număr care poate fi exprimat ca coeficientul a două numere întregi:
ℚ = { n / m ; n , m ∈ℤ}
Zero poate fi scris ca un coeficient de două numere întregi.
De exemplu:
0 = 0/3
Deci zero este un număr rațional.
Este zero un număr pozitiv?
Un număr pozitiv este definit ca un număr mai mare decât zero:
x / 0
De exemplu:
5/ 0
Deoarece zero nu este mai mare decât zero, nu este un număr pozitiv.
Este zero un număr prim?
Numărul 0 nu este un număr prim.
Zero nu este un număr pozitiv și are un număr infinit de divizori.
Cel mai mic număr prim este 2.