Regulile componente

Reguli ale componentelor, legile exponentului și exemple.

• Ce este un exponent
• Regulile exponenților
• Calculator pentru exponenți

Ce este un exponent

Baza a ridicată la puterea lui n este egală cu înmulțirea a, n ori:

a ⁿ = a × a × ... × a

                    de n ori

a este baza și n este exponentul.

Exemple

3 ¹ = 3

3 ² = 3 × 3 = 9

3 ³ = 3 × 3 × 3 = 27

3 ⁴ = 3 × 3 × 3 × 3 = 81

3 ⁵ = 3 × 3 × 3 × 3 × 3 = 243

Regulile și proprietățile exponenților

Numele regulii	Regulă	Exemplu
Regulile produsului	a n ⋅ a m = a n + m	2 3 ⋅ 2 4 = 2 3 + 4 = 128
	a n ⋅ b n = ( a ⋅ b ) n	3 2 ⋅ 4 2 = (3⋅4) 2 = 144
Regulile coeficientului	a n / a m = a n - m	2 de 5 /2 3 = 2 devine 5-3 = 4
	a n / b n = ( a / b ) n	4 3 / cu 2 3 = (4/2) 3 = 8
Reguli de putere	( b n ) m = b n⋅m	(2 3 ) 2 = 2 3⋅2 = 64
	b n m = b ( n m )	2 3 2 = 2 ( 3 2 ) = 512
	m √ ( b n ) = b n / m	2 √ (2 6 ) = 2 6/2 = 8
	b 1 / n = n √ b	8 1/3 = 3 √ 8 = 2
Exponenți negativi	b -n = 1 / b n	2 -3 = 1/2 3 = 0,125
Zero reguli	b 0 = 1	5 0 = 1
	0 n = 0, pentru n / 0	0 5 = 0
Una regulă	b 1 = b	5 1 = 5
	1 n = 1	1 5 = 1
Minus o regulă		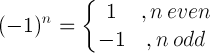(-1) 5 = -1
Regula derivată	( x n ) ' = n ⋅ x n -1	( x 3 ) ' = 3⋅ x 3-1
Regula integrală	∫ x n dx = x n +1 / ( n +1) + C	∫ x 2 dx = x 2 + 1 / (2 + 1) + C

Regulile produsului pentru exponenți

Regula produsului cu aceeași bază

a ⁿ ⋅ a ^m = a ^{n + m}

Exemplu:

2 ³ ⋅ 2 ⁴ = 2 ^{3 + 4} = 2 ⁷ = 2⋅2⋅2⋅2⋅2⋅2⋅2 = 128

Regula produsului cu același exponent

a ⁿ ⋅ b ⁿ = ( a ⋅ b ) ⁿ

Exemplu:

3 ² ⋅ 4 ² = (3⋅4) ² = 12 ² = 12⋅12 = 144

A se vedea: Multiplicarea exponenților

Regulile coeficientului exponenților

Regula cotientului cu aceeași bază

a ⁿ / a ^m = a ^{n - m}

Exemplu:

2 de ⁵ /2 ³ = 2 ^{devine 5-3} = 2 ² = 2⋅2 = 4

Regula cotientului cu același exponent

a ⁿ / b ⁿ = ( a / b ) ⁿ

Exemplu:

4 ³ /2 ³ = (4/2) ³ = 2 ³ = 2⋅2⋅2 = 8

A se vedea: Împărțirea exponenților

Regulile puterii exponenților

Regula puterii I

( a ⁿ ) ^m = a ^n⋅m

Exemplu:

(2 ³ ) ² = 2 ^3⋅2 = 2 ⁶ = 2⋅2⋅2⋅2⋅2⋅2 = 64

Regula puterii II

_a n ^m _{= a} ( n ^m )

Exemplu:

₂ 3 ² _{= 2} (3 ² ) _{= 2} (3⋅3) _{= 2} 9 _{= 2⋅2⋅2⋅2⋅2⋅2⋅2⋅2⋅2 = 512}

Regula puterii cu radicali

^m √ ( a ⁿ ) = a ^{n / m}

Exemplu:

² √ (2 ⁶ ) = 2 ^6/2 = 2 ³ = 2⋅2⋅2 = 8

Regula exponenților negativi

b ^-n = 1 / b ⁿ

Exemplu:

2 ^-3 = 1/2 ³ = 1 / (2⋅2⋅2) = 1/8 = 0,125

A se vedea: Exponenți negativi

Calculator de componente ►

Vezi si

• Adăugarea de exponenți
• Împărțirea exponenților
• Exponenți fracționari
• Multiplicarea exponenților
• Exponenți negativi
• Simplificarea exponenților
• Exponent zero
• Calculator de componente
• Calculator de logaritm
• Calculator de creștere exponențială
• Calculator antilog
• log (x) reguli
• ln (x) reguli
• e constantă