Funcția Arccos (x)
Arccos (x), cos -1 (x), funcție de cosinus invers .
Definiția Arccos
Arccozinul lui x este definit ca funcția cosinusului invers al lui x când -1≤x≤1.
Când cosinusul lui y este egal cu x:
cos y = x
Atunci arccosinul lui x este egal cu funcția inversă a cosinusului lui x, care este egală cu y:
arccos x = cos -1 x = y
(Aici cos -1 x înseamnă cosinusul invers și nu înseamnă cosinus pentru puterea lui -1).
Exemplu
arccos 1 = cos -1 1 = 0 rad = 0 °
Graficul arccos
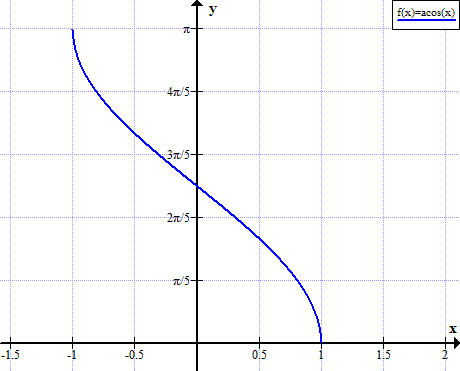
Regulile Arccos
| Numele regulii | Regulă |
|---|---|
| Cosinusul arccosinei | cos (arccos x ) = x |
| Arccosine de cosinus | arccos (cos x ) = x + 2 k π, când k ∈ℤ ( k este întreg) |
| Arccos de argument negativ | arccos (- x ) = π - arccos x = 180 ° - arccos x |
| Unghiuri complementare | arccos x = π / 2 - arcsin x = 90 ° - arcsin x |
| Arccos sum | arccos ( α ) + arccos ( β ) = arccos ( αβ - √ (1- α 2 ) (1- β 2 ) ) |
| Diferența Arccos | arccos ( α ) - arccos ( β ) = arccos ( αβ + √ (1- α 2 ) (1- β 2 ) ) |
| Arccos al păcatului lui x | arccos (sin x ) = - x - (2 k +0,5) π |
| Păcatul arccosinei | |
| Tangenta arccosinei | 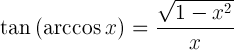 |
| Derivat de arccosine | 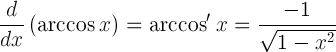 |
| Integrală nedefinită a arccosinei | |
Masa Arccos
| x | arccos (x) (rad) |
arccos (x) (°) |
|---|---|---|
| -1 | π | 180 ° |
| -√ cu 3 / cu 2 | 5π / 6 | 150 ° |
| -√ cu 2 / cu 2 | 3π / 4 | 135 ° |
| -1/2 | 2π / 3 | 120 ° |
| 0 | π / 2 | 90 ° |
| 1/2 | π / 3 | 60 ° |
| √ cu 2 / cu 2 | π / 4 | 45 ° |
| √ cu 3 / cu 2 | π / 6 | 30 ° |
| 1 | 0 | 0 ° |
Vezi si
- Funcția cosinusului
- Funcția Arcsine
- Arctanfuncție
- Calculator Arccos
- Convertor de radiani în grade
- Arccos de 0
- Arccos de 1
- Arccos de 2
- Arccos de 3
- Arccos de cos
- Arccos al păcatului
- Derivat arccos
- Graficul Arccos
- Cos de arccos
- Păcatul de arccos
- Tan de arccos