Förväntningsvärde
I sannolikhet och statistik är förväntningen eller det förväntade värdet det vägda medelvärdet för en slumpmässig variabel.
Förväntan på kontinuerlig slumpmässig variabel
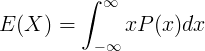
E ( X ) är förväntningsvärdet för den kontinuerliga slumpmässiga variabeln X
x är värdet på den kontinuerliga slumpmässiga variabeln X
P ( x ) är sannolikhetsdensitetsfunktionen
Förväntan på diskret slumpmässig variabel
![]()
E ( X ) är förväntningsvärdet för den kontinuerliga slumpmässiga variabeln X
x är värdet på den kontinuerliga slumpmässiga variabeln X
P ( x ) är sannolikhetsfunktionen för X
Förväntade egenskaper
Linjäritet
När a är konstant och X är Y slumpmässiga variabler:
E ( aX ) = aE ( X )
E ( X + Y ) = E ( X ) + E ( Y )
Konstant
När c är konstant:
E ( c ) = c
Produkt
När X och Y är oberoende slumpmässiga variabler:
E ( X ⋅Y ) = E ( X ) ⋅ E ( Y )
villkorad förväntan
Se även
SANNLIKHET & STATISTIK
- Grundläggande sannolikhet
- Förväntan
- Variation
- Standardavvikelse
- Sannolikhetsfördelning
- Normal distribution
- Statistik symboler
SNABBBORD