Grundläggande sannolikhetsformler

 

Sannolikhetsområde

0 ≤ P ( A ) ≤ 1

Regel för kompletterande händelser

P ( A C ) + P ( A ) = 1

Tilläggsregel

P (A∪B) = P (A) + P (B) - P (A∩B)

Ojämna händelser

Händelserna A och B är oskiljaktiga iff

P (A∩B) = 0

Villkorlig sannolikhet

P (A | B) = P (A∩B) / P (B)

Bayes formel

P (A | B) = P (B | A) ⋅ P (A) / P (B)

Oberoende händelser

Händelserna A och B är oberoende iff

P (A∩B) = P (A) ⋅ P (B)

Kumulativ fördelningsfunktion

F X ( x ) = P ( X ≤ x )

Sannolikhetsfunktion

summa (i = 1..n, P (X = x (i)) = 1

Sannolikhetsdensitetsfunktion

fX (x) = dFX (x) / dx

FX (x) = integrerad (-inf..x, fX (y) * dy)

FX (x) = summa (k = 1..x, P (X = k))

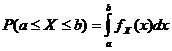
P (a <= X <= b) = integrerad (a..b, fX (x) * dx)

integral (-inf..inf, fX (x) * dx) = 1

 

Kovarians

Cox (X, Y) = E (X-ux) (Y-uy) = E (XY) - ux * uy

Korrelation

corr (X, Y) = Cov (X, Y) / (Std (X) * Std (Y))

 

Bernoulli: 0-fel 1-framgång

Geometrisk: 0-fel 1-framgång

Hypergeometrisk: N-objekt med K-framgångsobjekt, n-objekt tas.

 

 

 
 
SANNLIKHET & STATISTIK
SNABBBORD