Sannolikhetsfördelning

I sannolikhet och statistik är distribution en egenskap hos en slumpmässig variabel, beskriver sannolikheten för den slumpmässiga variabeln i varje värde.

Varje distribution har en viss funktion för sannolikhetstäthet och sannolikhetsfördelning.

Även om det finns ett obegränsat antal sannolikhetsfördelningar, finns det flera vanliga distributioner som används.

Kumulativ fördelningsfunktion

Sannolikhetsfördelningen beskrivs av den kumulativa fördelningsfunktionen F (x),

vilket är sannolikheten för att slumpmässig variabel X får ett värde som är mindre än eller lika med x:

F ( x ) = P ( X ≤ x )

Kontinuerlig distribution

Den kumulativa fördelningsfunktionen F (x) beräknas genom integrering av sannolikhetsdensitetsfunktionen f (u) för kontinuerlig slumpmässig variabel X.

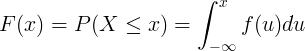
Diskret distribution

Den kumulativa fördelningsfunktionen F (x) beräknas genom summering av sannolikhetsmassfunktionen P (u) för diskret slumpmässig variabel X.

Kontinuerlig distributionstabell

Kontinuerlig fördelning är fördelningen av en kontinuerlig slumpmässig variabel.

Exempel på kontinuerlig distribution

...

Kontinuerlig distributionstabell

Distributionsnamn Distributionssymbol Sannolikhetsdensitetsfunktion (pdf) Betyda Variation
   

f X ( x )

μ = E ( X )

σ 2 = Var ( X )
Normal / gaussisk

X ~ N (μ, σ 2 )

 \ frac {1} {\ sigma \ sqrt {2 \ pi}} e ^ {- \ frac {(x- \ mu) ^ 2} {2 \ sigma ^ 2}} μ σ 2
Enhetlig

X ~ U ( a , b )

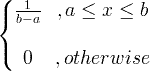 \ börja {Bmatrix} \ frac {1} {ba} &, a \ leq x \ leq b \\ & \\ 0 &, annars \ slut {matris} \ frac {(ba) ^ 2} {12}
Exponentiell X ~ exp (λ) \ börja {Bmatrix} \ lambda e ^ {- \ lambda x} & x \ geq 0 \\ 0 & x <0 \ end {matrix} \ frac {1} {\ lambda} \ frac {1} {\ lambda ^ 2}
Gamma X ~ gamma ( c , λ) 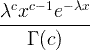\ frac {\ lambda ^ cx ^ {c-1} e ^ {- \ lambda x}} {\ Gamma (c)}

x / 0, c / 0, λ/ 0

 \ frac {c} {\ lambda} \ frac {c} {\ lambda ^ 2}
Chi kvadrat

X ~ χ 2 ( k )

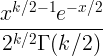 \ frac {x ^ {k / 2-1} e ^ {- x / 2}} {2 ^ {k / 2} \ Gamma (k / 2)}

k

2 k
Wishart        
F

X ~ F ( k 1 , k 2 )

      
Beta        
Weibull        
Log-normal

X ~ LN (μ, σ 2 )

      
Rayleigh        
Cauchy        
Dirichlet        
Laplace        
Avgift        
Ris        
Studentens t        

Diskret fördelningstabell

Diskret fördelning är fördelningen av en diskret slumpmässig variabel.

Exempel på diskret distribution

...

Diskret fördelningstabell

Distributionsnamn Distributionssymbol Sannolikhetsmassfunktion (pmf) Betyda Variation
    f x ( k ) = P ( X = k )

k = 0,1,2, ...

 E ( x ) Var ( x )
Binom

X ~ Fack ( n , p )

 \ binom {n} {k} p ^ {k} (1-p) ^ {nk}

np

np (1- p )
Poisson

X ~ Poisson (λ)

λ ≥ 0

λ

λ

Enhetlig

X ~ U ( a, b )

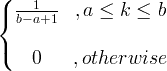 \ börja {Bmatrix} \ frac {1} {b-a + 1} &, a \ leq k \ leq b \\ & \\ 0 &, annars \ end {matrix} \ frac {a + b} {2} \ frac {(b-a + 1) ^ {2} -1} {12}
Geometrisk

X ~ Geom ( p )

 p (1-p) ^ {k}

\ frac {1-p} {p}

\ frac {1-p} {p ^ 2}
Hypergeometrisk

X ~ HG ( N , K , n )

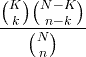N = 0,1,2, ...

K = 0,1, .., N

n = 0,1, ..., N

 \ frac {nK} {N} \ frac {nK (NK) (Nn)} {N ^ 2 (N-1)}
Bernoulli

X ~ Bern ( p )

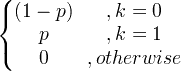 \ börja {Bmatrix} (1-p) &, k = 0 \\ p &, k = 1 \\ 0 &, annars \ slut {matris}

p

p (1- p )

 

Se även

SANNLIKHET & STATISTIK
SNABBBORD