e స్థిరాంకం

e స్థిరాంకం లేదా ఐలర్ సంఖ్య గణిత స్థిరాంకం. ఇ స్థిరాంకం నిజమైన మరియు అహేతుక సంఖ్య.

e = 2.718281828459 ...

ఇ యొక్క నిర్వచనం
ఇ యొక్క లక్షణాలు
బేస్ ఇ లోగరిథం
ఘాతాంక ఫంక్షన్
ఐలర్ యొక్క సూత్రం

ఇ యొక్క నిర్వచనం

ఇ స్థిరాంకం పరిమితిగా నిర్వచించబడింది:

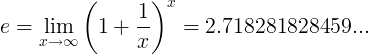
$e = \ lim_ {x \ rightarrow \ infty} \ left (1+ \ frac {1} {x} \ right) ^ x = 2.718281828459 ...$

ప్రత్యామ్నాయ నిర్వచనాలు

ఇ స్థిరాంకం పరిమితిగా నిర్వచించబడింది:

$e = \ lim_ {x \ కుడివైపు 0} \ ఎడమ (1+ \ కుడి x) ^ \ frac {1} {x}$

ఇ స్థిరాంకం అనంత శ్రేణిగా నిర్వచించబడింది:

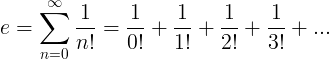
$e = \ sum_ {n = 0} ^ {\ infty} \ frac {1} {n!} = \ frac {1} {0!} + \ frac {1} {1!} + \ frac {1} {. 2!} + \ ఫ్రాక్ {1} {3!} + ...$

ఇ యొక్క లక్షణాలు

ఇ యొక్క పరస్పరం

ఇ యొక్క పరస్పర పరిమితి:

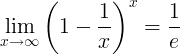
$\ lim_ {x \ rightarrow \ infty} \ ఎడమ (1- \ frac {1} {x} \ కుడి) ^ x = \ frac {1} {e}$

ఇ యొక్క ఉత్పన్నాలు

ఘాతాంక ఫంక్షన్ యొక్క ఉత్పన్నం ఘాతాంక ఫంక్షన్:

( e ^x ) '= e ^x

సహజ లాగరిథం ఫంక్షన్ యొక్క ఉత్పన్నం పరస్పర విధి:

(లాగ్ _ఇ x ) '= (ln x )' = 1 / x

ఇ యొక్క సమగ్రతలు

ఎక్స్పోనెన్షియల్ ఫంక్షన్ e ^x యొక్క నిరవధిక సమగ్ర ఘాతాంక ఫంక్షన్ e ^x .

∫ ఇ ^x DX = ఇ ^x + సి

సహజ లాగరిథం ఫంక్షన్ లాగ్ _e x యొక్క నిరవధిక సమగ్రత :

Log _e x dx = ∫ ln x dx = x ln x - x + c

పరస్పర ఫంక్షన్ 1 / x యొక్క 1 నుండి e వరకు ఖచ్చితమైన సమగ్ర 1:

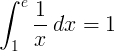
$\ int_ {1} ^ {e} \ frac {1} {x} \: dx = 1$

బేస్ ఇ లోగరిథం

సంఖ్య x యొక్క సహజ లాగరిథం x యొక్క బేస్ ఇ లాగరిథమ్‌గా నిర్వచించబడింది:

ln x = లాగ్ _ఇ x

ఘాతాంక ఫంక్షన్

ఘాతాంక ఫంక్షన్ ఇలా నిర్వచించబడింది:

f ( x ) = exp ( x ) = e ^x

ఐలర్ యొక్క సూత్రం

సంక్లిష్ట సంఖ్య e ^iθ కి గుర్తింపు ఉంది:

ఇ ^iθ = cos ( θ ) + నేను పాపం ( θ )

నేను inary హాత్మక యూనిట్ (-1 యొక్క వర్గమూలం).

Any ఏదైనా వాస్తవ సంఖ్య.