సున్నా సంఖ్య (0)
సున్నా సంఖ్య నిర్వచనం
జీరో అనేది గణితంలో పరిమాణం లేదా శూన్య పరిమాణాన్ని వివరించడానికి ఉపయోగించే సంఖ్య.
టేబుల్పై 2 ఆపిల్ల ఉన్నప్పుడు మరియు మేము 2 ఆపిల్లను తీసుకున్నప్పుడు, టేబుల్పై సున్నా ఆపిల్ల ఉన్నాయని చెప్పగలను.
సున్నా సంఖ్య సానుకూల సంఖ్య కాదు మరియు ప్రతికూల సంఖ్య కాదు.
సున్నా ఇతర సంఖ్యలలో ప్లేస్హోల్డర్ అంకె (ఉదా: 40,103, 170).
సున్నా సంఖ్యనా?
సున్నా ఒక సంఖ్య. ఇది సానుకూల లేదా ప్రతికూల సంఖ్య కాదు.
సున్నా అంకె
సంఖ్యలను వ్రాసేటప్పుడు సున్నా అంకెను ప్లేస్హోల్డర్గా ఉపయోగిస్తారు.
ఉదాహరణకి:
204 = 2 × 100 + 0 × 10 + 4 × 1
సున్నా సంఖ్య చరిత్ర
సున్నా సంఖ్యను ఎవరు కనుగొన్నారు?
ఆధునిక 0 చిహ్నం 6 వ శతాబ్దంలో భారతదేశంలో కనుగొనబడింది, తరువాత దీనిని పర్షియన్లు మరియు అరబ్బులు మరియు తరువాత ఐరోపాలో ఉపయోగించారు.
సున్నా యొక్క చిహ్నం
సున్నా సంఖ్యను 0 గుర్తుతో సూచిస్తారు .
అరబిక్ సంఖ్యా వ్యవస్థ ٠ గుర్తును ఉపయోగిస్తుంది.
సున్నా సంఖ్య లక్షణాలు
x ఏదైనా సంఖ్యను సూచిస్తుంది.
| ఆపరేషన్ | నియమం | ఉదాహరణ |
|---|---|---|
అదనంగా |
x + 0 = x |
3 + 0 = 3 |
వ్యవకలనం |
x - 0 = x |
3 - 0 = 3 |
గుణకారం |
x × 0 = 0 |
5 × 0 = 0 |
విభజన |
0 ÷ x = 0 , x ≠ 0 ఉన్నప్పుడు |
0 5 = 0 |
| x ÷ 0 నిర్వచించబడలేదు |
5 ÷ 0 నిర్వచించబడలేదు |
|
ఘాతాంకం |
0 x = 0 |
0 5 = 0 |
| x 0 = 1 |
5 0 = 1 |
|
రూట్ |
√ 0 = 0 |
|
లోగరిథం |
లాగ్ బి (0) నిర్వచించబడలేదు |
|
| |
||
కారకం |
0! = 1 |
|
సైన్ |
sin 0º = 0 |
|
కొసైన్ |
cos 0º = 1 |
|
టాంజెంట్ |
తాన్ 0º = 0 |
|
ఉత్పన్నం |
0 '= 0 |
|
సమగ్ర |
0 d x = 0 + C. |
|
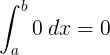 |
సున్నా అదనంగా
సంఖ్య ప్లస్ సున్నా యొక్క సంఖ్య సంఖ్యకు సమానం:
x + 0 = x
ఉదాహరణకి:
5 + 0 = 5
సున్నా వ్యవకలనం
సంఖ్య మైనస్ సున్నా యొక్క వ్యవకలనం సంఖ్యకు సమానం:
x - 0 = x
ఉదాహరణకి:
5 - 0 = 5
సున్నా ద్వారా గుణకారం
సున్నా సంఖ్య యొక్క గుణకారం సున్నాకి సమానం:
x × 0 = 0
ఉదాహరణకి:
5 × 0 = 0
సంఖ్య సున్నాతో విభజించబడింది
సున్నా ద్వారా సంఖ్య యొక్క విభజన నిర్వచించబడలేదు:
x ÷ 0 నిర్వచించబడలేదు
ఉదాహరణకి:
5 ÷ 0 నిర్వచించబడలేదు
సున్నా సంఖ్యతో విభజించబడింది
సంఖ్య ద్వారా సున్నా యొక్క విభజన సున్నా:
0 ÷ x = 0
ఉదాహరణకి:
0 5 = 0
సున్నా శక్తికి సంఖ్య
సున్నా పెంచిన సంఖ్య యొక్క శక్తి ఒకటి:
x 0 = 1
ఉదాహరణకి:
5 0 = 1
సున్నా యొక్క లోగరిథం
సున్నా యొక్క బేస్ బి లాగరిథం నిర్వచించబడలేదు:
లాగ్ బి (0) నిర్వచించబడలేదు
సున్నా పొందడానికి బేస్ b ని పెంచగల సంఖ్య లేదు.
X సున్నాగా మారినప్పుడు x యొక్క బేస్ బి లాగరిథం యొక్క పరిమితి మాత్రమే మైనస్ అనంతం:
![]()
సున్నా కలిగి ఉన్న సెట్లు
జీరో అనేది సహజ సంఖ్యలు, పూర్ణాంక సంఖ్యలు, వాస్తవ సంఖ్యలు మరియు సంక్లిష్ట సంఖ్యల సెట్ల యొక్క ఒక మూలకం:
| సెట్ | సభ్యత్వ సంజ్ఞామానాన్ని సెట్ చేయండి |
|---|---|
| సహజ సంఖ్యలు (ప్రతికూలంగా లేవు) | 0 ∈ 0 |
| పూర్ణాంక సంఖ్యలు | 0 |
| వాస్తవ సంఖ్యలు | 0 |
| సంక్లిష్ట సంఖ్యలు | 0 |
| హేతుబద్ధ సంఖ్యలు | 0 |
సున్నా సరి లేదా బేసి సంఖ్య?
సరి సంఖ్యల సమితి:
{..., -10, -8, -6, -4, -2, 0, 2, 4, 6, 8, 10, ...}
బేసి సంఖ్యల సమితి:
{..., -9, -7, -5, -3, -1, 1, 3, 5, 7, 9, ...}
సున్నా 2 యొక్క పూర్ణాంక గుణకం:
0 × 2 = 0
సమం సంఖ్యల సమితిలో జీరో సభ్యుడు:
0 ∈ {2 క , క }}
కాబట్టి సున్నా సమాన సంఖ్య మరియు బేసి సంఖ్య కాదు.
సున్నా సహజ సంఖ్యనా?
సహజ సంఖ్యల సెట్కు రెండు నిర్వచనాలు ఉన్నాయి.
ప్రతికూలత లేని పూర్ణాంకాల సమితి:
ℕ 0 = {0,1,2,3,4,5,6,7,8, ...}
సానుకూల పూర్ణాంకాల సమితి:
ℕ 1 = {1,2,3,4,5,6,7,8, ...}
ప్రతికూల కాని పూర్ణాంకాల సమితిలో జీరో సభ్యుడు:
0 ∈ 0
సానుకూల పూర్ణాంకాల సమితిలో జీరో సభ్యుడు కాదు:
0 ∉ 1
సున్నా మొత్తం సంఖ్యనా?
మొత్తం సంఖ్యలకు మూడు నిర్వచనాలు ఉన్నాయి:
పూర్ణాంక సంఖ్యల సమితి:
= {0,1,2,3,4,5,6,7,8, ...}
ప్రతికూలత లేని పూర్ణాంకాల సమితి:
ℕ 0 = {0,1,2,3,4,5,6,7,8, ...}
సానుకూల పూర్ణాంకాల సమితి:
ℕ 1 = {1,2,3,4,5,6,7,8, ...}
సున్నా పూర్ణాంక సంఖ్యల సమితి మరియు ప్రతికూల కాని పూర్ణాంకాల సమితిలో సభ్యుడు:
0
0 ∈ 0
సానుకూల పూర్ణాంకాల సమితిలో జీరో సభ్యుడు కాదు:
0 ∉ 1
సున్నా పూర్ణాంక సంఖ్యనా?
పూర్ణాంక సంఖ్యల సమితి:
= {0,1,2,3,4,5,6,7,8, ...}
సున్నా పూర్ణాంక సంఖ్యల సమితిలో సభ్యుడు:
0
కాబట్టి సున్నా పూర్ణాంక సంఖ్య.
సున్నా హేతుబద్ధ సంఖ్యనా?
హేతుబద్ధ సంఖ్య రెండు పూర్ణాంక సంఖ్యల మూలంగా వ్యక్తీకరించబడే సంఖ్య:
= { N / m ; n , m ∈ℤ}
సున్నాన్ని రెండు పూర్ణాంక సంఖ్యల మూలకంగా వ్రాయవచ్చు.
ఉదాహరణకి:
0 = 0/3
కాబట్టి సున్నా ఒక హేతుబద్ధ సంఖ్య.
సున్నా సానుకూల సంఖ్యనా?
సానుకూల సంఖ్య సున్నా కంటే ఎక్కువ ఉన్న సంఖ్యగా నిర్వచించబడింది:
x / 0
ఉదాహరణకి:
5/ 0
సున్నా సున్నా కంటే ఎక్కువ కాదు కాబట్టి, ఇది సానుకూల సంఖ్య కాదు.
సున్నా ప్రధాన సంఖ్యనా?
సంఖ్య 0 ప్రధాన సంఖ్య కాదు.
సున్నా సానుకూల సంఖ్య కాదు మరియు అనంతమైన విభజనలను కలిగి ఉంటుంది.
అత్యల్ప ప్రధాన సంఖ్య 2.