ఘాతాంక నియమాలు

ఘాతాంక నియమాలు, ఘాతాంక చట్టాలు మరియు ఉదాహరణలు.

• ఘాతాంకం అంటే ఏమిటి
• ఘాతాంక నియమాలు
• ఘాతాంకాలు కాలిక్యులేటర్

ఘాతాంకం అంటే ఏమిటి

N యొక్క శక్తికి పెంచబడిన ఆధారం a, n రెట్లు గుణించటానికి సమానం:

a ⁿ = a × a × ... × a

                    n సార్లు

a బేస్ మరియు n ఘాతాంకం.

ఉదాహరణలు

3 ¹ = 3

3 ² = 3 × 3 = 9

3 ³ = 3 × 3 × 3 = 27

3 ⁴ = 3 × 3 × 3 × 3 = 81

3 ⁵ = 3 × 3 × 3 × 3 × 3 = 243

ఘాతాంకాలు నియమాలు మరియు లక్షణాలు

నియమం పేరు	నియమం	ఉదాహరణ
ఉత్పత్తి నియమాలు	ఒక n ⋅ ఒక m = ఒక n + m	2 3 ⋅ 2 4 = 2 3 + 4 = 128
	ఒక n ⋅ బి n = ( ఒక ⋅ బి ) n	3 2 ⋅ 4 2 = (3⋅4) 2 = 144
పరిమాణ నియమాలు	a n / a m = a n - m	2 5 /2 3 = 2 5-3 = 4
	a n / b n = ( a / b ) n	4 3 /2 3 = (4/2) 3 = 8
శక్తి నియమాలు	( b n ) m = b n⋅m	(2 3 ) 2 = 2 3⋅2 = 64
	b n m = b ( n m )	2 3 2 = 2 ( 3 2 ) = 512
	m ( b n ) = b n / m	2 (2 6 ) = 2 6/2 = 8
	b 1 / n = n √ బి	8 1/3 = 3 √ 8 = 2
ప్రతికూల ఘాతాంకాలు	b -n = 1 / b n	2 -3 = 1/2 3 = 0.125
సున్నా నియమాలు	b 0 = 1	5 0 = 1
	0 n = 0, n / 0 కోసం	0 5 = 0
ఒక నియమాలు	b 1 = బి	5 1 = 5
	1 n = 1	1 5 = 1
మైనస్ వన్ రూల్		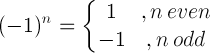(-1) 5 = -1
ఉత్పన్న నియమం	( X n ) ' = n ⋅ x n -1	( x 3 ) ' = 3⋅ x 3-1
సమగ్ర నియమం	∫ x n DX = x n +1 / ( n +1) + సి	∫ x 2 DX = x 2 + 1 / (2 + 1) + సి

ఉత్పత్తి నియమాలు

ఒకే బేస్ ఉన్న ఉత్పత్తి నియమం

ఒక ⁿ ⋅ ఒక ^m = ఒక ^{n + m}

ఉదాహరణ:

2 ³ 2 ⁴ = 2 ^{3 + 4} = 2 ⁷ = 2⋅2⋅2⋅2⋅2⋅2⋅2 = 128

అదే ఘాతాంకంతో ఉత్పత్తి నియమం

ఒక ⁿ ⋅ బి ⁿ = ( ఒక ⋅ బి ) ⁿ

ఉదాహరణ:

3 ² ⋅ 4 ² = (3⋅4) ² = 12 ² = 12⋅12 = 144

చూడండి: గుణకాలు ఘాతాంకాలు

ఘాతాంకాలు నియమ నిబంధనలు

ఒకే బేస్ ఉన్న పరిమాణ నియమం

a ⁿ / a ^m = a ^{n - m}

ఉదాహరణ:

2 ⁵ /2 ³ = 2 ^5-3 = 2 ² = 2⋅2 = 4

అదే ఘాతాంకంతో పరిమాణ నియమం

a ⁿ / b ⁿ = ( a / b ) ⁿ

ఉదాహరణ:

4 ³ /2 ³ = (4/2) ³ = 2 ³ = 2⋅2⋅2 = 8

చూడండి: ఘాతాంకాలను విభజించడం

శక్తి నియమాలు

శక్తి నియమం I.

( a ⁿ ) ^m = a ^n⋅m

ఉదాహరణ:

(2 ³ ) ² = 2 ^3⋅2 = 2 ⁶ = 2⋅2⋅2⋅2⋅2⋅2 = 64

శక్తి నియమం II

_a n ^m _{= a} ( n ^m )

ఉదాహరణ:

₂ 3 ² _{= 2} (3 ² ) _{= 2} (3⋅3) _{= 2} 9 _{= 2⋅2⋅2⋅2⋅2⋅2⋅2⋅2⋅2 = 512}

రాడికల్స్‌తో శక్తి నియమం

^m √ ( a ⁿ ) = a ^{n / m}

ఉదాహరణ:

² (2 ⁶ ) = 2 ^6/2 = 2 ³ = 2⋅2⋅2 = 8

ప్రతికూల ఘాతాంకాలు నియమం

b ^-n = 1 / b ⁿ

ఉదాహరణ:

2 ^-3 = 1/2 ³ = 1 / (2⋅2⋅2) = 1/8 = 0.125

చూడండి: ప్రతికూల ఘాతాంకాలు

ఘాతాంక కాలిక్యులేటర్

ఇది కూడ చూడు

• ఘాతాంకాలను కలుపుతోంది
• ఘాతాంకాలను విభజించడం
• పాక్షిక ఘాతాంకాలు
• ఘాతాంకాలు గుణించడం
• ప్రతికూల ఘాతాంకాలు
• ఘాతాంకాలను సులభతరం చేస్తుంది
• జీరో ఘాతాంకం
• ఘాతాంక కాలిక్యులేటర్
• లోగరిథం కాలిక్యులేటర్
• ఘాతాంక వృద్ధి కాలిక్యులేటర్
• యాంటిలాగ్ కాలిక్యులేటర్
• లాగ్ (x) నియమాలు
• ln (x) నియమాలు
• e స్థిరాంకం