e คงที่
ค่าคงที่หรือจำนวนของออยเลอร์เป็นค่าคงที่ทางคณิตศาสตร์ ค่าคงที่คือจำนวนจริงและไม่ลงตัว
จ = 2.718281828459 ...
คำจำกัดความของ e
ค่าคงที่ถูกกำหนดเป็นขีด จำกัด :
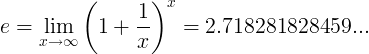
นิยามทางเลือก
ค่าคงที่ถูกกำหนดเป็นขีด จำกัด :
![]()
ค่าคงที่ e ถูกกำหนดให้เป็นอนุกรมอนันต์:
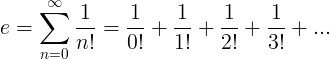
คุณสมบัติของ e
ซึ่งกันและกันของ e
ซึ่งกันและกันของ e คือขีด จำกัด :
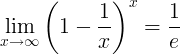
อนุพันธ์ของ e
อนุพันธ์ของฟังก์ชันเอกซ์โพเนนเชียลคือฟังก์ชันเลขชี้กำลัง:
( จx ) '= จx
อนุพันธ์ของฟังก์ชันลอการิทึมธรรมชาติคือฟังก์ชันซึ่งกันและกัน:
(บันทึกe x ) '= (ln x )' = 1 / x
ปริพันธ์ของ e
ซึ่งเป็นส่วนประกอบสำคัญที่ไม่แน่นอนของการชี้แจงฟังก์ชั่นอีxเป็นฟังก์ชันชี้แจง E x
∫ e x dx = e x + c
อินทิกรัลไม่ จำกัด ของฟังก์ชันลอการิทึมธรรมชาติบันทึกe xคือ:
∫บันทึกe x dx = ∫ ln x dx = x ln x - x + c
อินทิกรัลที่แน่นอนจาก 1 ถึง e ของฟังก์ชันซึ่งกันและกัน 1 / x คือ 1:
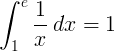
ฐาน e ลอการิทึม
ลอการิทึมธรรมชาติของจำนวน x ถูกกำหนดให้เป็นลอการิทึมฐาน e ของ x:
ln x = บันทึกe x
ฟังก์ชันเอกซ์โปเนนเชียล
ฟังก์ชันเลขชี้กำลังถูกกำหนดให้เป็น:
f ( x ) = exp ( x ) = e x
สูตรของออยเลอร์
จำนวนเชิงซ้อนe iθมีตัวตน:
e iθ = cos ( θ ) + ฉันบาป ( θ )
ผมคือหน่วยจินตภาพ (รากที่สองของ -1)
θคือจำนวนจริงใด ๆ
ดูสิ่งนี้ด้วย
- e 2.71828183 เป็นอย่างไร
- กฎลอการิทึม
- ลอการิทึมธรรมชาติ
- กฎเลขชี้กำลัง
- การแจกแจงปกติ
- Pi คงที่
- ค่าคงที่ - วิกิพีเดีย
NUMBERS
- e คงที่
- เลขชี้กำลัง
- หมายเลขฟีโบนักชี
- ตารางการคูณ
- ระบบตัวเลข
- ส่วนต่อล้าน (ppm)
- ต่อล้าน (‰)
- เปอร์เซ็นต์ (%)
- จำนวนเฉพาะ
- เลขศูนย์
ตารางอย่างรวดเร็ว