ลอการิทึมธรรมชาติ - ln (x)
ลอการิทึมธรรมชาติคือลอการิทึมของฐาน e ของจำนวน
- นิยามลอการิทึมธรรมชาติ (ln)
- กฎและคุณสมบัติลอการิทึมธรรมชาติ (ln)
- ลอการิทึมเชิงซ้อน
- กราฟของ ln (x)
- ตารางลอการิทึมธรรมชาติ (ln)
- เครื่องคิดเลขลอการิทึมธรรมชาติ
ความหมายของลอการิทึมธรรมชาติ
เมื่อไหร่
e y = x
จากนั้นลอการิทึมฐาน e ของ x คือ
ln ( x ) = บันทึกe ( x ) = y
อีคงที่หรือหมายเลขออยเลอร์คือ:
e ≈ 2.71828183
Ln เป็นฟังก์ชันผกผันของฟังก์ชันเอกซ์โพเนนเชียล
LN ฟังก์ชันลอการิทึมธรรมชาติ (x) เป็นฟังก์ชันผกผันของฟังก์ชันเลขชี้กำลัง E x
สำหรับ x/ 0,
f ( f -1 ( x )) = e ln ( x ) = x
หรือ
f -1 ( f ( x )) = ln ( อีx ) = x
กฎและคุณสมบัติลอการิทึมธรรมชาติ
| ชื่อกฎ | กฎ | ตัวอย่าง |
|---|---|---|
กฎผลิตภัณฑ์ |
ln ( x ∙ y ) = ln ( x ) + ln ( y ) |
ln (3 ∙ 7) = ln (3) + ln (7) |
กฎความฉลาด |
ln ( x / y ) = ln ( x ) - ln ( y ) |
LN (3 / 7) = LN (3) - LN (7) |
กฎอำนาจ |
ln ( x y ) = y ∙ ln ( x ) |
ln (2 8 ) = 8 ∙ ln (2) |
อนุพันธ์ ln |
f ( x ) = ln ( x ) ⇒ f ' ( x ) = 1 / x | |
ln อินทิกรัล |
∫ ln ( x ) dx = x ∙ (ln ( x ) - 1) + C | |
ln ของจำนวนลบ |
ln ( x ) ไม่ได้กำหนดไว้เมื่อ x ≤ 0 | |
ln ของศูนย์ |
ln (0) ไม่ได้กำหนด | |
ln ของหนึ่ง |
ln (1) = 0 | |
ln ของอินฟินิตี้ |
lim ln ( x ) = ∞ เมื่อx →∞ | |
| เอกลักษณ์ของออยเลอร์ | ln (-1) = ฉัน π |
กฎผลิตภัณฑ์ลอการิทึม
ลอการิทึมของการคูณ x และ y คือผลรวมของลอการิทึมของ x และลอการิทึมของ y
บันทึกb ( x ∙ y ) = บันทึกb ( x ) +บันทึกb ( y )
ตัวอย่างเช่น:
บันทึก10 (3 ∙ 7) = บันทึก10 (3) +บันทึก10 (7)
กฎผลหารลอการิทึม
ลอการิทึมของการหาร x และ y คือผลต่างของลอการิทึมของ x และลอการิทึมของ y
บันทึกb ( x / y ) = บันทึกb ( x ) -บันทึกb ( y )
ตัวอย่างเช่น:
เข้าสู่ระบบ10 (3 / 7) เข้าสู่ระบบ = 10 (3) -เข้าสู่ระบบ10 (7)
กฎอำนาจลอการิทึม
ลอการิทึมของ x ยกกำลัง y คือ y คูณลอการิทึมของ x
บันทึกb ( x y ) = y ∙บันทึกb ( x )
ตัวอย่างเช่น:
บันทึก10 (2 8 ) = 8 ∙บันทึก10 (2)
อนุพันธ์ของลอการิทึมธรรมชาติ
อนุพันธ์ของฟังก์ชันลอการิทึมธรรมชาติคือฟังก์ชันซึ่งกันและกัน
เมื่อไหร่
f ( x ) = ln ( x )
อนุพันธ์ของ f (x) คือ:
f ' ( x ) = 1 / x
อินทิกรัลของลอการิทึมธรรมชาติ
อินทิกรัลของฟังก์ชันลอการิทึมธรรมชาติกำหนดโดย:
เมื่อไหร่
f ( x ) = ln ( x )
อินทิกรัลของ f (x) คือ:
∫ f ( x ) dx = ∫ ln ( x ) dx = x ∙ (ln ( x ) - 1) + C
Ln ของ 0
ไม่ได้กำหนดลอการิทึมธรรมชาติของศูนย์:
ln (0) ไม่ได้กำหนด
ขีด จำกัด ใกล้ 0 ของลอการิทึมธรรมชาติของ x เมื่อ x เข้าใกล้ศูนย์จะเป็นลบอินฟินิตี้:
![]()
Ln จาก 1
ลอการิทึมธรรมชาติของหนึ่งเป็นศูนย์:
ln (1) = 0
Ln ของอินฟินิตี้
ขีด จำกัด ของลอการิทึมธรรมชาติของอินฟินิตี้เมื่อ x เข้าใกล้อินฟินิตี้เท่ากับอินฟินิตี้:
lim ln ( x ) = ∞ เมื่อ x →∞
ลอการิทึมเชิงซ้อน
สำหรับจำนวนเชิงซ้อน z:
z = re iθ = x + iy
ลอการิทึมเชิงซ้อนจะเป็น (n = ...- 2, -1,0,1,2, ... ):
บันทึกz = ln ( r ) + i ( θ + 2nπ ) = ln (√ ( x 2 + y 2 )) + i · arctan ( y / x ))
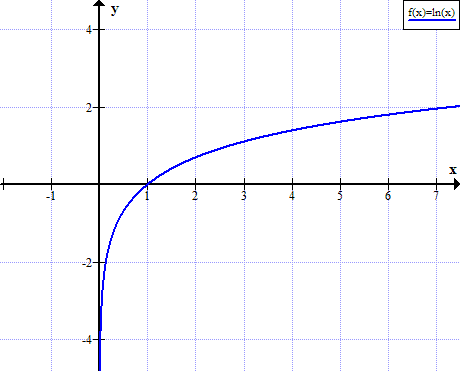
กราฟของ ln (x)
ln (x) ไม่ได้กำหนดไว้สำหรับค่าจริงที่ไม่ใช่บวกของ x:
ตารางลอการิทึมธรรมชาติ
| x | ln x |
|---|---|
| 0 | ไม่ได้กำหนด |
| 0 + | - ∞ |
| 0.0001 | -9.210340 |
| 0.001 | -6.907755 |
| 0.01 | -4.605170 |
| 0.1 | -2.302585 |
| 1 | 0 |
| 2 | 0.693147 |
| e ≈ 2.7183 | 1 |
| 3 | 1.098612 |
| 4 | 1.386294 |
| 5 | 1.609438 |
| 6 | 1.791759 |
| 7 | 1.945910 |
| 8 | 2.079442 |
| 9 | 2.197225 |
| 10 | 2.302585 |
| 20 | 2.995732 |
| 30 | 3.401197 |
| 40 | 3.688879 |
| 50 | 3.912023 |
| 60 | 4.094345 |
| 70 | 4.248495 |
| 80 | 4.382027 |
| 90 | 4.499810 |
| 100 | 4.605170 |
| 200 | 5.298317 |
| 300 | 5.703782 |
| 400 | 5.991465 |
| 500 | 6.214608 |
| 600 | 6.396930 |
| 700 | 6.551080 |
| 800 | 6.684612 |
| 900 | 6.802395 |
| 1,000 | 6.907755 |
| 10,000 | 9.210340 |
ดูสิ่งนี้ด้วย
- ลอการิทึม (log)
- เครื่องคิดเลขลอการิทึมธรรมชาติ
- ลอการิทึมธรรมชาติของศูนย์
- ลอการิทึมธรรมชาติของหนึ่ง
- ลอการิทึมธรรมชาติของ e
- ลอการิทึมธรรมชาติของอินฟินิตี้
- ลอการิทึมธรรมชาติของจำนวนลบ
- ฟังก์ชันผกผัน Ln
- กราฟ ln (x)
- ตารางลอการิทึมธรรมชาติ
- เครื่องคิดเลขลอการิทึม
- e คงที่
พีชคณิต
ตารางอย่างรวดเร็ว