Beklenti Değeri

Olasılık ve istatistikte, beklenti veya beklenen değer , rastgele bir değişkenin ağırlıklı ortalama değeridir.

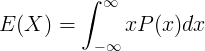
$E (X) = \ int _ {- \ infty} ^ {\ infty} xP (x) dx$

E ( X ), sürekli rastgele değişken X'in beklenti değeridir

x sürekli rastgele değişken X'in değeridir

P ( x ) olasılık yoğunluk fonksiyonudur

$E (X) = \ toplam_ {i} ^ {} x_iP (x)$

E ( X ), sürekli rastgele değişken X'in beklenti değeridir

x sürekli rastgele değişken X'in değeridir

P ( x ), X'in olasılık kütle fonksiyonudur

A sabit ve X olduğunda, Y rastgele değişkenlerdir:

E ( aX ) = aE ( X )

E ( X + Y ) = E ( X ) + E ( Y )

C sabit olduğunda:

E ( c ) = c

X ve Y bağımsız rastgele değişkenler olduğunda:

E ( X ⋅Y ) = E ( X ) ⋅ E ( Y )

Ayrıca bakınız