Olasılık dağılımı
Olasılık ve istatistikte dağılım , rastgele bir değişkenin bir özelliğidir, her bir değerdeki rastgele değişkenin olasılığını açıklar.
Her dağılımın belirli bir olasılık yoğunluk işlevi ve olasılık dağılımı işlevi vardır.
Belirsiz sayıda olasılık dağılımı olmasına rağmen, kullanımda birkaç yaygın dağılım vardır.
Kümülatif dağılım fonksiyonu
Olasılık dağılımı, kümülatif dağılım fonksiyonu F (x) ile tanımlanır,
bu, rastgele X değişkeninin x'e eşit veya daha küçük bir değer elde etme olasılığıdır:
F ( x ) = P ( X ≤ x )
Sürekli dağıtım
Kümülatif dağılım fonksiyonu F (x), sürekli rastgele değişken X'in olasılık yoğunluk fonksiyonu f (u) entegrasyonu ile hesaplanır.
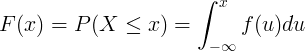
Ayrık dağıtım
Kümülatif dağılım fonksiyonu F (x), ayrık rasgele değişken X'in olasılık kütle fonksiyonu P (u) 'nun toplanmasıyla hesaplanır.
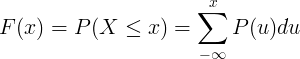
Sürekli dağılım tablosu
Sürekli dağılım, sürekli bir rasgele değişkenin dağılımıdır.
Sürekli dağıtım örneği
...
Sürekli dağılım tablosu
| Dağıtım adı | Dağıtım sembolü | Olasılık yoğunluk işlevi (pdf) | Anlamına gelmek | Varyans |
|---|---|---|---|---|
| f X ( x ) |
μ = E ( X ) |
σ 2 = Var ( X ) |
||
| Normal / gauss | X ~ N (μ, σ 2 ) |
|
μ | σ 2 |
| Üniforma | X ~ U ( a , b ) |
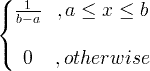 |
|
|
| Üstel | X ~ exp (λ) | |
|
|
| Gama | X ~ gama ( c , λ) | 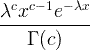 x / 0, c / 0, λ/ 0 |
|
|
| Chi kare | X ~ χ 2 ( k ) |
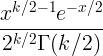 |
k |
2 k |
| Wishart | ||||
| F | X ~ F ( k 1 , k 2 ) |
|||
| Beta | ||||
| Weibull | ||||
| Normal günlük | X ~ LN (μ, σ 2 ) |
|||
| Rayleigh | ||||
| Cauchy | ||||
| Dirichlet | ||||
| Laplace | ||||
| Levy | ||||
| Pirinç | ||||
| Öğrenci t |
Ayrık dağılım tablosu
Kesikli dağılım, ayrık bir rastgele değişkenin dağılımıdır.
Ayrık dağıtım örneği
...
Ayrık dağılım tablosu
| Dağıtım adı | Dağıtım sembolü | Olasılık kütle işlevi (pmf) | Anlamına gelmek | Varyans | |
|---|---|---|---|---|---|
| f x ( k ) = P ( X = k ) k = 0,1,2, ... |
E ( x ) | Var ( x ) | |||
| Binom | X ~ Bin ( n , p ) |
|
np |
np (1- p ) |
|
| Poisson | X ~ Poisson (λ) |
|
λ ≥ 0 |
λ |
λ |
| Üniforma | X ~ U ( a, b ) |
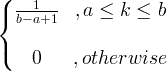 |
|
|
|
| Geometrik | X ~ Geom ( p ) |
|
|
|
|
| Hiper geometrik | X ~ HG ( N , K , n ) |
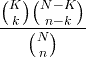 |
N = 0,1,2, ... K = 0,1, .., N n = 0,1, ..., N |
|
|
| Bernoulli | X ~ Bern ( p ) |
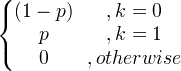 |
p |
p (1- p ) |
|
Ayrıca bakınız
OLASILIK VE İSTATİSTİK
- Temel olasılık
- Beklenti
- Varyans
- Standart sapma
- Olasılık dağılımı
- Normal dağılım
- İstatistik sembolleri
HIZLI TABLOLAR