Varyans

Olasılık ve istatistikte, rastgele bir değişkenin varyansı , ortalama değerden uzaklığın karesinin ortalama değeridir. Rastgele değişkenin ortalama değerin yakınında nasıl dağıldığını temsil eder. Küçük varyans, rastgele değişkenin ortalama değerin yakınında dağıldığını gösterir. Büyük varyans, rastgele değişkenin ortalama değerden uzağa dağıldığını gösterir. Örneğin, normal dağılımla, dar çan eğrisi küçük, geniş çan eğrisi büyük değişkenliğe sahip olacaktır.

Varyans tanımı

Rastgele değişken X'in varyansı, X farkının karelerinin beklenen değeri ve beklenen değer μ'dir.

σ 2 = Var ( X ) = E [( X - μ ) 2 ]

Varyansın tanımından elde edebiliriz

σ 2 = Var ( X ) = E ( X 2 ) - μ 2

Sürekli rastgele değişkenin varyansı

Ortalama değeri μ ve olasılık yoğunluk fonksiyonu f (x) olan sürekli rastgele değişken için:

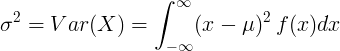
\ sigma ^ 2 = Var (X) = \ int _ {- \ infty} ^ {\ infty} (x- \ mu) ^ 2 \: f (x) dx

veya

Var (X) = \ sol [\ int _ {- \ infty} ^ {\ infty} x ^ 2 \: f (x) dx \ sağ] - \ mu ^ 2

Kesikli rastgele değişkenin varyansı

Ortalama değeri μ ve olasılık kütle fonksiyonu P (x) olan ayrık rastgele değişken X için:

\ sigma ^ 2 = Var (X) = \ sum_ {i} ^ {} (x_i- \ mu _X) ^ 2P_X (x_i)

veya

Var (X) = \ sol [\ sum_ {i} ^ {} x_i ^ 2P (x_i) \ sağ] - \ mu ^ 2

Varyansın özellikleri

X ve Y bağımsız rastgele değişkenler olduğunda:

Var ( X + Y ) = Var ( X ) + Var ( Y )

 

Standart sapma ►

 

Ayrıca bakınız

OLASILIK VE İSTATİSTİK
HIZLI TABLOLAR