e константа

Константа або число Ейлера є математичною константою. Постійна e - дійсне та ірраціональне число.

e = 2,718281828459 ...

Визначення е
Властивості e
Основа е логарифм
Експоненціальна функція
Формула Ейлера

Визначення е

Константа e визначається як межа:

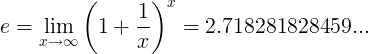
$e = \ lim_ {x \ rightarrow \ infty} \ ліворуч (1+ \ frac {1} {x} \ праворуч) ^ x = 2,718281828459 ...$

Альтернативні визначення

Константа e визначається як межа:

$e = \ lim_ {x \ rightarrow 0} \ вліво (1+ \ вправо x) ^ \ frac {1} {x}$

Постійна e визначається як нескінченний ряд:

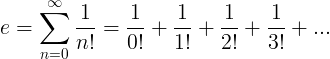
$e = \ sum_ {n = 0} ^ {\ infty} \ frac {1} {n!} = \ frac {1} {0!} + \ frac {1} {1!} + \ frac {1} { 2!} + \ Frac {1} {3!} + ...$

Властивості e

Взаємний e

Взаємне значення e - це межа:

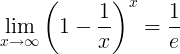
$\ lim_ {x \ rightarrow \ infty} \ ліворуч (1- \ frac {1} {x} \ right) ^ x = \ frac {1} {e}$

Похідні від e

Похідною експоненціальної функції є експоненціальна функція:

( e ^x ) '= e ^x

Похідною функції натурального логарифму є зворотна функція:

(log _e x ) '= (ln x )' = 1 / x

Інтеграли e

Невизначений інтеграл від експоненціальної функції e ^x є показниковою функцією e ^x .

∫ e ^x dx = e ^x + c

Невизначений інтеграл функції натурального логарифму log _e x є:

∫ log _e x dx = ∫ ln x dx = x ln x - x + c

Певним інтегралом від 1 до e зворотної функції 1 / x є 1:

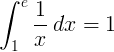
$\ int_ {1} ^ {e} \ frac {1} {x} \: dx = 1$

Основа е логарифм

Натуральний логарифм числа x визначається як базовий e логарифм x:

ln x = log _e x

Експоненціальна функція

Експоненціальна функція визначається як:

f ( x ) = exp ( x ) = e ^x

Формула Ейлера

Комплексне число e ^iθ має тотожність:

e ^iθ = cos ( θ ) + i sin ( θ )

i - уявна одиниця (квадратний корінь з -1).

θ - будь-яке дійсне число.