Нульове число (0)
- Визначення нульового числа
- Історія нульового числа
- Властивості нульового числа
- Набори, що містять нуль
Визначення нульового числа
Нуль - це число, яке використовується в математиці для опису кількості чи нульової величини.
Коли на столі лежать 2 яблука, і ми беремо 2 яблука, можна сказати, що на столі нуль яблук.
Нульове число не є додатним чи не від’ємним числом.
Нуль - це також цифра-заповнювач в інших числах (наприклад: 40,103, 170).
Нуль - це число?
Нуль - це число. Це не позитивне, ані негативне число.
Нульова цифра
Нульова цифра використовується як заповнювач під час запису цифр.
Наприклад:
204 = 2 × 100 + 0 × 10 + 4 × 1
Історія нульового числа
Хто винайшов нульове число?
Сучасний символ 0 був винайдений в Індії в 6 столітті, пізніше використовувався персами та арабами, а потім і в Європі.
Символ нуля
Нульове число позначається символом 0 .
В арабській цифровій системі використовується символ ٠.
Властивості нульового числа
x являє собою будь-яке число.
| Операція | Правило | Приклад |
|---|---|---|
Додавання |
x + 0 = x |
3 + 0 = 3 |
Віднімання |
x - 0 = x |
3 - 0 = 3 |
Множення |
x × 0 = 0 |
5 × 0 = 0 |
Відділ |
0 ÷ x = 0 , коли x ≠ 0 |
0 ÷ 5 = 0 |
| x ÷ 0 не визначено |
5 ÷ 0 не визначено |
|
Потенціювання |
0 x = 0 |
0 5 = 0 |
| x 0 = 1 |
5 0 = 1 |
|
Корінь |
√ 0 = 0 |
|
Логарифм |
log b (0) не визначено |
|
| |
||
Факториал |
0! = 1 |
|
Синус |
sin 0º = 0 |
|
Косинус |
cos 0º = 1 |
|
Дотична |
загар 0º = 0 |
|
Похідна |
0 '= 0 |
|
Цілісний |
∫ 0 d x = 0 + C |
|
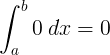 |
Нульове додавання
Додавання числа плюс нуль дорівнює числу:
x + 0 = x
Наприклад:
5 + 0 = 5
Нульове віднімання
Віднімання числа, мінус нуль, дорівнює числу:
x - 0 = x
Наприклад:
5 - 0 = 5
Множення на нуль
Множення числа на нуль дорівнює нулю:
x × 0 = 0
Наприклад:
5 × 0 = 0
Число, поділене на нуль
Ділення числа на нуль не визначено:
x ÷ 0 не визначено
Наприклад:
5 ÷ 0 не визначено
Нуль, поділений на число
Ділення нуля на число дорівнює нулю:
0 ÷ x = 0
Наприклад:
0 ÷ 5 = 0
Число до нульової потужності
Ступінь числа, піднятого на нуль, одиниця:
x 0 = 1
Наприклад:
5 0 = 1
Логарифм нуля
Базовий логарифм нуля невизначений:
log b (0) не визначено
Немає числа, за допомогою якого ми можемо підняти основу b, щоб отримати нуль.
Тільки межа базового b-логарифму x, коли x сходиться до нуля, це мінус нескінченність:
![]()
Набори, що містять нуль
Нуль - це елемент натуральних чисел, цілих чисел, дійсних чисел та наборів комплексних чисел:
| Встановити | Встановити позначення членства |
|---|---|
| Натуральні числа (невід’ємні) | 0 ∈ ℕ 0 |
| Цілі числа | 0 ∈ ℤ |
| Дійсні числа | 0 ∈ ℝ |
| Комплексні числа | 0 ∈ ℂ |
| Раціональні числа | 0 ∈ ℚ |
Нульове парне чи непарне число?
Набір парних чисел:
{..., -10, -8, -6, -4, -2, 0, 2, 4, 6, 8, 10, ...}
Набір непарних чисел:
{..., -9, -7, -5, -3, -1, 1, 3, 5, 7, 9, ...}
Нуль - ціле число, кратне 2:
0 × 2 = 0
Нуль є членом набору парних чисел:
0 ∈ {2 k , k ∈ℤ}
Отже, нуль - це парне число, а не непарне.
Чи є нуль натуральним числом?
Існує два визначення для набору натуральних чисел.
Набір невід’ємних цілих чисел:
ℕ 0 = {0,1,2,3,4,5,6,7,8, ...}
Набір цілих додатних чисел:
ℕ 1 = {1,2,3,4,5,6,7,8, ...}
Нуль є членом набору цілих невід’ємних чисел:
0 ∈ ℕ 0
Нуль не є членом набору натуральних чисел:
0 ∉ ℕ 1
Нуль - це ціле число?
Існують три визначення для цілих чисел:
Набір цілих чисел:
ℤ = {0,1,2,3,4,5,6,7,8, ...}
Набір невід’ємних цілих чисел:
ℕ 0 = {0,1,2,3,4,5,6,7,8, ...}
Набір цілих додатних чисел:
ℕ 1 = {1,2,3,4,5,6,7,8, ...}
Нуль є членом набору цілих чисел і набору невід'ємних цілих чисел:
0 ∈ ℤ
0 ∈ ℕ 0
Нуль не є членом набору натуральних чисел:
0 ∉ ℕ 1
Чи є нуль цілим числом?
Набір цілих чисел:
ℤ = {0,1,2,3,4,5,6,7,8, ...}
Нуль є членом набору цілих чисел:
0 ∈ ℤ
Отже, нуль - це ціле число.
Чи є нуль раціональним числом?
Раціональне число - це число, яке можна виразити як частку двох цілих чисел:
ℚ = { н / м ; n , m ∈ℤ}
Нуль можна записати як частку двох цілих чисел.
Наприклад:
0 = 0/3
Отже, нуль - це раціональне число.
Чи нуль - це додатне число?
Позитивне число визначається як число, яке більше нуля:
x / 0
Наприклад:
5/ 0
Оскільки нуль не більше нуля, це не додатне число.
Чи є нуль простим числом?
Число 0 не є простим числом.
Нуль не є додатним числом і має нескінченну кількість дільників.
Найнижче просте число - 2.