صفر نمبر (0)

• صفر نمبر کی تعریف
  • کیا صفر ایک نمبر ہے؟
  • زیرو ہندسہ
• صفر نمبر کی تاریخ
  • صفر نمبر کس نے ایجاد کیا؟
  • علامت صفر
• صفر نمبر کی خصوصیات
  • صفر کے علاوہ
  • زیرو گھٹاؤ
  • صفر سے ضرب
  • تعداد صفر سے تقسیم ہوا
  • زیرو ایک نمبر سے تقسیم ہوا
  • صفر طاقت کی تعداد
  • لوگرتھم صفر ہے
• سیٹیں جو صفر پر مشتمل ہیں
  • کیا صفر مساوی یا عجیب تعداد ہے؟
  • کیا صفر قدرتی نمبر ہے؟
  • کیا صفر پوری تعداد ہے؟
  • کیا صفر ایک عدد نمبر ہے؟
  • کیا صفر ایک عقلی نمبر ہے؟
  • کیا صفر مثبت نمبر ہے؟
  • کیا صفر اول نمبر ہے؟

صفر نمبر کی تعریف

زیرو ایک ایسی تعداد ہے جس میں ریاضی میں کوئی مقدار یا کالعدم مقدار کی وضاحت نہیں کی جاتی ہے۔

جب میز پر 2 سیب ہوتے ہیں اور ہم 2 سیب لیتے ہیں تو ہم کہہ سکتے ہیں کہ میز پر صفر سیب موجود ہیں۔

صفر نمبر مثبت نمبر نہیں اور منفی نمبر نہیں ہے۔

صفر دوسری نمبروں میں پلیس ہولڈر ہندسہ بھی ہے (جیسے: 40،103 ، 170)

کیا صفر ایک نمبر ہے؟

زیرو ایک نمبر ہے۔ یہ مثبت نہیں ہے اور نہ ہی منفی تعداد۔

زیرو ہندسہ

نمبر لکھتے وقت صفر ہندسے کو پلیس ہولڈر کے طور پر استعمال کیا جاتا ہے۔

مثال کے طور پر:

204 = 2 × 100 + 0 × 10 + 4 × 1

صفر نمبر کی تاریخ

صفر نمبر کس نے ایجاد کیا؟

جدید 0 علامت ہندوستان میں 6 ویں صدی میں ایجاد ہوئی تھی ، جسے فارسیوں اور عربوں نے بعد میں یوروپ میں استعمال کیا۔

علامت صفر

صفر کی تعداد 0 کی علامت کے ساتھ دی گئی ہے۔

عربی کے اعدادی نظام میں ٠ علامت استعمال ہوتی ہے۔

صفر نمبر کی خصوصیات

x کسی بھی تعداد کی نمائندگی کرتا ہے۔

آپریشن	قاعدہ	مثال
اضافہ	x + 0 = x	3 + 0 = 3
گھٹانا	x - 0 = x	3 - 0 = 3
ضرب	x × 0 = 0	5 × 0 = 0
ڈویژن	0 ÷ x = 0 ، جب x ≠ 0	0 ÷ 5 = 0
	x ÷ 0  غیر متعینہ ہے	5 ÷ 0 غیر متعینہ ہے
کفارہ	0 x = 0	0 5 = 0
	x 0 = 1	5 0 = 1
جڑ	. 0 = 0
لوگرتھم	لاگ بی (0) غیر متعینہ ہے
فیکٹریل	0! = 1
سائن	گناہ 0º = 0
کوسن	کیونکہ 0º = 1
ٹینجینٹ	ٹین 0º = 0
ماخوذ	0 '= 0
لازمی	∫ 0 d x = 0 + C

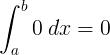صفر کے علاوہ

کسی بھی تعداد کے علاوہ صفر کا اضافہ کرنا اعداد کے برابر ہے:

x + 0 = x

مثال کے طور پر:

5 + 0 = 5

زیرو گھٹاؤ

ایک نمبر مائنس صفر کا گھٹائو تعداد کے برابر ہے:

x - 0 = x

مثال کے طور پر:

5 - 0 = 5

صفر سے ضرب

کئی بار صفر کی ضرب صفر کے برابر ہے۔

x × 0 = 0

مثال کے طور پر:

5 × 0 = 0

تعداد صفر سے تقسیم ہوا

کسی تعداد کی صفر کے لحاظ سے تقسیم کی وضاحت نہیں کی گئی ہے۔

x ÷ 0 غیر متعینہ ہے

مثال کے طور پر:

5 ÷ 0 غیر متعینہ ہے

زیرو ایک نمبر سے تقسیم ہوا

ایک صفر کا ایک نمبر کے لحاظ سے تقسیم صفر ہے:

0 ÷ x = 0

مثال کے طور پر:

0 ÷ 5 = 0

صفر طاقت کی تعداد

صفر کے ذریعہ اٹھائے گئے عدد کی طاقت ایک ہے۔

x ⁰ = 1

مثال کے طور پر:

5 ⁰ = 1

لوگرتھم صفر ہے

بیرو بی لاگرتھم صفر کی وضاحت نہیں کی گئی ہے

لاگ _بی (0) غیر متعینہ ہے

کوئی تعداد نہیں ہے کہ ہم صفر حاصل کرنے کے لئے بیس بی کو بڑھاسکیں۔

x کے بیس بی لوگرتھم کی صرف حد ، جب ایکس صفر میں تبدیل ہوجاتا ہے منفی انفینٹی ہوتا ہے:

سیٹیں جو صفر پر مشتمل ہیں

صفر قدرتی اعداد ، عدد اعداد ، حقیقی تعداد اور پیچیدہ نمبروں کا مجموعہ ہے۔

سیٹ	رکنیت کی نشاندہی کریں
قدرتی نمبر (غیر منفی)	0 ∈ ℕ 0
عددی نمبر	0 ∈ ℤ
اصل نمبر	0 ∈ ℝ
پیچیدہ نمبر	0 ∈ ℂ
عقلی نمبر	0 ∈ ℚ

کیا صفر مساوی یا عجیب تعداد ہے؟

مساوی تعداد کا سیٹ یہ ہے:

{...، -10، -8، -6، -4، -2، 0، 2، 4، 6، 8، 10، ...}

عجیب تعداد کا مجموعہ یہ ہے:

{... ، -9 ، -7 ، -5 ، -3 ، -1 ، 1 ، 3 ، 5 ، 7 ، 9 ، ...}

صفر 2 کا پورا عدد متعدد ہے:

0 × 2 = 0

زیرو سیٹ کی جانے والی تعداد کی ایک ممبر ہے:

0 ∈ {2 ک ، ک ∈ℤ}

تو صفر ایک مساوی نمبر ہے نہ کہ عجیب تعداد۔

کیا صفر قدرتی نمبر ہے؟

قدرتی نمبروں کی دو تعریفیں ہیں۔

غیر منفی عدد کا سیٹ:

ℕ ₀ = {0،1،2،3،4،5،6،7،8، ...}

مثبت عدد کا سیٹ:

ℕ ₁ = {1،2،3،4،5،6،7،8، ...}

زیرو غیر منفی عددی اعداد و شمار کا ایک رکن ہے:

0 ∈ ℕ ₀

صفر مثبت انٹیجر کے سیٹ کا ممبر نہیں ہے:

0 ∉ ℕ ₁

کیا صفر پوری تعداد ہے؟

پوری تعداد کے لئے تین تعریفیں ہیں۔

عدد اعداد کا مجموعہ:

ℤ = {0،1،2،3،4،5،6،7،8، ...}

غیر منفی عدد کا سیٹ:

ℕ ₀ = {0،1،2،3،4،5،6،7،8، ...}

مثبت عدد کا سیٹ:

ℕ ₁ = {1،2،3،4،5،6،7،8، ...}

زیرو عددی نمبروں کے سیٹ اور غیر منفی عددی اعداد کا ایک سیٹ ہے:

0 ∈ ℤ

0 ∈ ℕ ₀

صفر مثبت انٹیجر کے سیٹ کا ممبر نہیں ہے:

0 ∉ ℕ ₁

کیا صفر ایک عدد نمبر ہے؟

عدد اعداد کا مجموعہ:

ℤ = {0،1،2،3،4،5،6،7،8، ...}

صفر عدد اعداد کے سیٹ کا ایک ممبر ہے:

0 ∈ ℤ

تو صفر ایک عدد نمبر ہے۔

کیا صفر ایک عقلی نمبر ہے؟

عقلی نمبر وہ نمبر ہے جس کا اظہار دو عدد اعداد کے فقرے کے طور پر کیا جاسکتا ہے:

ℚ = { n / ایم ؛ این ، ایم ∈ℤ}

صفر کو دو عدد اعداد کے فقرے کے طور پر لکھا جاسکتا ہے۔

مثال کے طور پر:

0 = 0/3

تو صفر ایک عقلی نمبر ہے۔

کیا صفر مثبت نمبر ہے؟

ایک مثبت تعداد کو ایک ایسی تعداد کے طور پر بیان کیا جاتا ہے جو صفر سے زیادہ ہو:

x / 0

مثال کے طور پر:

5/ 0

چونکہ صفر صفر سے زیادہ نہیں ہے ، لہذا یہ ایک مثبت تعداد نہیں ہے۔

کیا صفر اول نمبر ہے؟

نمبر 0 کوئی بنیادی نمبر نہیں ہے۔

زیرو ایک مثبت تعداد نہیں ہے اور اس میں تفرقوں کی لامحدود تعداد ہے۔

سب سے کم تعداد 2 ہے۔

 

---

بھی دیکھو

• ای مستقل
• فیکٹریل
• لوگرتھم
• ماخوذ