e không đổi

Hằng số e hay số Euler là một hằng số toán học. Hằng số e là số thực và số vô tỉ.

e = 2,718281828459 ...

Định nghĩa của e
Thuộc tính của e
Lôgarit cơ số e
Hàm số mũ
Công thức của Euler

Định nghĩa của e

Hằng số e được định nghĩa là giới hạn:

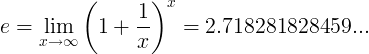
$e = \ lim_ {x \ rightarrow \ infty} \ left (1+ \ frac {1} {x} \ right) ^ x = 2.718281828459 ...$

Định nghĩa thay thế

Hằng số e được định nghĩa là giới hạn:

$e = \ lim_ {x \ rightarrow 0} \ left (1+ \ right x) ^ \ frac {1} {x}$

Hằng số e được định nghĩa là chuỗi vô hạn:

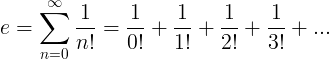
$e = \ sum_ {n = 0} ^ {\ infty} \ frac {1} {n!} = \ frac {1} {0!} + \ frac {1} {1!} + \ frac {1} { 2!} + \ Frac {1} {3!} + ...$

Thuộc tính của e

Đối ứng của e

Số nghịch đảo của e là giới hạn:

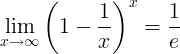
$\ lim_ {x \ rightarrow \ infty} \ left (1- \ frac {1} {x} \ right) ^ x = \ frac {1} {e}$

Các dẫn xuất của e

Đạo hàm của hàm số mũ là hàm số mũ:

( e ^x ) '= e ^x

Đạo hàm của hàm số logarit tự nhiên là hàm nghịch biến:

(log _e x ) '= (ln x )' = 1 / x

Tích phân của e

Tích phân không xác định của hàm số mũ e ^x là hàm số mũ e ^x .

∫ e ^x dx = e ^x + c

Tích phân không xác định của hàm logarit tự nhiên log _e x là:

∫ log _e x dx = ∫ ln x dx = x ln x - x + c

Tích phân xác định từ 1 đến e của hàm nghịch biến 1 / x là 1:

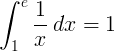
$\ int_ {1} ^ {e} \ frac {1} {x} \: dx = 1$

Lôgarit cơ số e

Lôgarit tự nhiên của một số x được định nghĩa là lôgarit cơ số e của x:

ln x = log _e x

Hàm số mũ

Hàm mũ được định nghĩa là:

f ( x ) = exp ( x ) = e ^x

Công thức của Euler

Số phức e ^iθ có dạng:

e ^iθ = cos ( θ ) + i sin ( θ )

i là đơn vị ảo (căn bậc hai của -1).

θ là bất kỳ số thực nào.