Số 0 (0)
Định nghĩa số 0
Số không là một số được sử dụng trong toán học để mô tả số lượng không hoặc số lượng rỗng.
Khi có 2 quả táo trên bàn và chúng ta lấy 2 quả táo, chúng ta có thể nói rằng không có quả táo nào trên bàn.
Số 0 không phải là số dương và không phải là số âm.
Số 0 cũng là một chữ số giữ chỗ trong các số khác (ví dụ: 40,103, 170).
Số 0 có phải là số không?
Số không là một số. Nó không phải là số dương cũng không phải là số âm.
Chữ số 0
Chữ số 0 được dùng làm chỗ dành sẵn khi viết số.
Ví dụ:
204 = 2 × 100 + 0 × 10 + 4 × 1
Lịch sử số 0
Ai là người phát minh ra số 0?
Biểu tượng số 0 hiện đại được phát minh ở Ấn Độ vào thế kỷ thứ 6, được người Ba Tư và Ả Rập sử dụng sau đó ở châu Âu.
Biểu tượng của số không
Số 0 được ký hiệu bằng ký hiệu 0 .
Hệ thống chữ số Ả Rập sử dụng ký hiệu ٠.
Thuộc tính số 0
x đại diện cho bất kỳ số nào.
| Hoạt động | Qui định | Thí dụ |
|---|---|---|
Thêm vào |
x + 0 = x |
3 + 0 = 3 |
Phép trừ |
x - 0 = x |
3 - 0 = 3 |
Phép nhân |
x × 0 = 0 |
5 × 0 = 0 |
Sư đoàn |
0 ÷ x = 0 , khi x ≠ 0 |
0 ÷ 5 = 0 |
| x ÷ 0 là không xác định |
5 ÷ 0 là không xác định |
|
Luỹ thừa |
0 x = 0 |
0 5 = 0 |
| x 0 = 1 |
5 0 = 1 |
|
Nguồn gốc |
√ 0 = 0 |
|
Lôgarit |
log b (0) là không xác định |
|
| |
||
yếu tố |
0! = 1 |
|
Sin |
sin 0º = 0 |
|
Cô sin |
cos 0º = 1 |
|
Tiếp tuyến |
tan 0º = 0 |
|
Phát sinh |
0 '= 0 |
|
Tích phân |
∫ 0 d x = 0 + C |
|
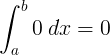 |
Không bổ sung
Phép cộng của một số với số không được bằng số:
x + 0 = x
Ví dụ:
5 + 0 = 5
Phép trừ 0
Phép trừ một số trừ số 0 được số:
x - 0 = x
Ví dụ:
5 - 0 = 5
Nhân với 0
Phép nhân một số với số 0 được bằng 0:
x × 0 = 0
Ví dụ:
5 × 0 = 0
Số chia cho 0
Phép chia một số cho số 0 không được xác định:
x ÷ 0 là không xác định
Ví dụ:
5 ÷ 0 là không xác định
Số 0 chia cho một số
Phép chia số 0 cho một số bằng 0:
0 ÷ x = 0
Ví dụ:
0 ÷ 5 = 0
Số đến công suất 0
Lũy thừa của một số được nâng lên bằng 0 là một:
x 0 = 1
Ví dụ:
5 0 = 1
Lôgarit của 0
Lôgarit b cơ số 0 là không xác định:
log b (0) là không xác định
Không có số nào mà chúng ta có thể nâng cơ số b lên để nhận được số không.
Chỉ giới hạn của logarit cơ số b của x, khi x hội tụ 0 thì trừ đi vô cùng:
![]()
Bộ chứa số 0
Số 0 là phần tử của tập hợp số tự nhiên, số nguyên, số thực và số phức:
| Đặt | Đặt ký hiệu thành viên |
|---|---|
| Số tự nhiên (không âm) | 0 ∈ ℕ 0 |
| Số nguyên | 0 ∈ ℤ |
| Số thực | 0 ∈ ℝ |
| Số phức | 0 ∈ ℂ |
| Số hữu tỉ | 0 ∈ ℚ |
Số 0 là số chẵn hay số lẻ?
Tập hợp các số chẵn là:
{..., -10, -8, -6, -4, -2, 0, 2, 4, 6, 8, 10, ...}
Tập hợp các số lẻ là:
{..., -9, -7, -5, -3, -1, 1, 3, 5, 7, 9, ...}
Số không là bội số nguyên của 2:
0 × 2 = 0
Số 0 là một thành viên của tập hợp số chẵn:
0 ∈ {2 k , k ∈ℤ}
Vì vậy số 0 là số chẵn chứ không phải số lẻ.
Số 0 có phải là số tự nhiên không?
Có hai định nghĩa cho tập hợp số tự nhiên.
Tập hợp các số nguyên không âm:
ℕ 0 = {0,1,2,3,4,5,6,7,8, ...}
Tập hợp các số nguyên dương:
ℕ 1 = {1,2,3,4,5,6,7,8, ...}
Số 0 là một thành viên của tập hợp các số nguyên không âm:
0 ∈ ℕ 0
Số 0 không phải là thành viên của tập hợp các số nguyên dương:
0 ∉ ℕ 1
Số 0 có phải là số nguyên không?
Có ba định nghĩa cho các số nguyên:
Tập hợp các số nguyên:
ℤ = {0,1,2,3,4,5,6,7,8, ...}
Tập hợp các số nguyên không âm:
ℕ 0 = {0,1,2,3,4,5,6,7,8, ...}
Tập hợp các số nguyên dương:
ℕ 1 = {1,2,3,4,5,6,7,8, ...}
Số 0 là một thành viên của tập hợp các số nguyên và tập hợp các số nguyên không âm:
0 ∈ ℤ
0 ∈ ℕ 0
Số 0 không phải là thành viên của tập hợp các số nguyên dương:
0 ∉ ℕ 1
Số 0 có phải là số nguyên không?
Tập hợp các số nguyên:
ℤ = {0,1,2,3,4,5,6,7,8, ...}
Số 0 là một thành viên của tập hợp các số nguyên:
0 ∈ ℤ
Vì vậy, số không là một số nguyên.
Số 0 có phải là số hữu tỉ không?
Một số hữu tỉ là một số có thể được biểu thị bằng thương của hai số nguyên:
ℚ = { n / m ; n , m ∈ℤ}
Số 0 có thể được viết dưới dạng thương của hai số nguyên.
Ví dụ:
0 = 0/3
Vậy số 0 là một số hữu tỉ.
Số 0 có phải là số dương không?
Một số dương được định nghĩa là một số lớn hơn 0:
x / 0
Ví dụ:
5/ 0
Vì số 0 không lớn hơn 0 nên nó không phải là số dương.
Số 0 có phải là số nguyên tố không?
Số 0 không phải là số nguyên tố.
Số 0 không phải là số dương và có vô số ước số.
Số nguyên tố thấp nhất là 2.