Arccos（x）函数

Arccos（x），cos -1（x），反余弦函数。

Arccos定义

x的反余弦定义为当-1≤x≤1时x的反余弦函数。

当y的余弦等于x时：

cos y = x

然后x的反余弦等于x的反余弦函数，它等于y：

arccos x = cos -1 x = y

（此处cos -1 x表示反余弦，并不表示-1的幂的余弦）。

例

arccos 1 = cos -1 1 = 0 rad = 0°

arccos图

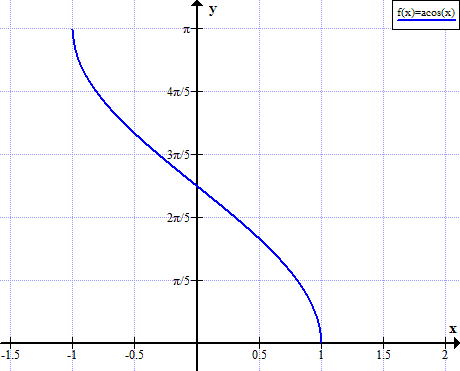
Arccos规则

规则名称 规则
反余弦的余弦 cos（arccos x）= x
余弦的反余弦 反余弦（COS X）= X + 2 ķ π，当ķ ∈ℤ（ķ是整数）
否定论的Arccos arccos（-x）=π-arccos x = 180°-arccos x
互补角 arccos x =π/ 2-反正弦x = 90°-反正弦x
Arccos总和 反余弦（α）+反余弦（β）=
   反余弦（αβ - √ （1- α 2）（1- β 2））
Arccos差异 反余弦（α） -反余弦（β）=
   反余弦（αβ + √ （1- α 2）（1- β 2））
x的罪恶Arccos arccos（sin x）=- x-（2 k +0.5）π
反余弦的正弦
反余弦正切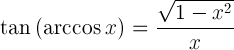
反余弦的衍生物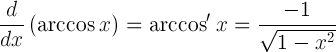
反余弦的不定积分

Arccos表

x arccos（x）

（rad）

 arccos（x）

（°）
-1 π 180°
-√ 3 /2 5π/ 6 150°
-√ 2 /2 3π/ 4 135°
-1/2 2π/ 3 120度
0 π/ 2 90°
1/2 π/ 3 60度
√ 2 /2 π/ 4 45°
√ 3 /2 π/ 6 30°
1 0 0度

 

也可以看看

三角法
快速表格