الرئيسية / الرياضيات / الاحتمالات /التباين

فرق

في الاحتمالات والإحصاءات ، تباين المتغير العشوائي هو متوسط قيمة المسافة المربعة من القيمة المتوسطة. يمثل كيفية توزيع المتغير العشوائي بالقرب من القيمة المتوسطة. يشير التباين الصغير إلى أن المتغير العشوائي يتم توزيعه بالقرب من متوسط القيمة. يشير التباين الكبير إلى أن المتغير العشوائي موزع بعيدًا عن متوسط القيمة. على سبيل المثال ، مع التوزيع الطبيعي ، سيكون لمنحنى الجرس الضيق تباين صغير وسيكون لمنحنى الجرس العريض تباين كبير.

تعريف التباين

تباين المتغير العشوائي X هو القيمة المتوقعة لمربعات فرق X والقيمة المتوقعة μ.

σ ² = Var ( X ) = E [( X - μ ) ² ]

من تعريف التباين يمكننا الحصول عليه

σ ² = Var ( X ) = E ( X ² ) - μ ²

تباين المتغير العشوائي المستمر

للمتغير العشوائي المستمر مع متوسط القيمة μ ودالة كثافة الاحتمال f (x):

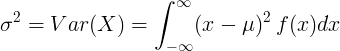
$\ سيجما ^ 2 = فار (X) = \ int _ {- \ infty} ^ {\ infty} (x- \ mu) ^ 2 \: f (x) dx$

أو

$Var (X) = \ left [\ int _ {- \ infty} ^ {\ infty} x ^ 2 \: f (x) dx \ right] - \ mu ^ 2$

تباين المتغير العشوائي المنفصل

للمتغير العشوائي X المنفصل ذي القيمة المتوسطة μ ووظيفة الكتلة الاحتمالية P (x):

$\ sigma ^ 2 = Var (X) = \ sum_ {i} ^ {} (x_i- \ mu _X) ^ 2P_X (x_i)$

أو

$Var (X) = \ left [\ sum_ {i} ^ {} x_i ^ 2P (x_i) \ right] - \ mu ^ 2$

خصائص التباين

عندما تكون X و Y متغيرات عشوائية مستقلة:

Var ( X + Y ) = Var ( X ) + Var ( Y )

الانحراف المعياري ►

أنظر أيضا

الاحتمالات والإحصاءات

جداول سريعة