الرئيسية / الرياضيات / الاحتمالية /الانحراف المعياري

الانحراف المعياري

في الاحتمالات والإحصاءات ، الانحراف المعياري لمتغير عشوائي هو متوسط مسافة متغير عشوائي من القيمة المتوسطة.

يمثل كيفية توزيع المتغير العشوائي بالقرب من القيمة المتوسطة. يشير الانحراف المعياري الصغير إلى أن المتغير العشوائي يتم توزيعه بالقرب من القيمة المتوسطة. يشير الانحراف المعياري الكبير إلى أن المتغير العشوائي موزع بعيدًا عن متوسط القيمة.

صيغة تعريف الانحراف المعياري

الانحراف المعياري هو الجذر التربيعي لتباين المتغير العشوائي X ، بمتوسط قيمة μ.

$\ sigma = std (X) = \ sqrt {Var (X)} = \ sqrt {E ((X- \ mu) ^ 2}$

من تعريف الانحراف المعياري يمكننا الحصول عليه

$\ sigma = std (X) = \ sqrt {E (X ^ 2) - \ mu ^ 2}$

الانحراف المعياري للمتغير العشوائي المستمر

للمتغير العشوائي المستمر مع متوسط القيمة μ ودالة كثافة الاحتمال f (x):

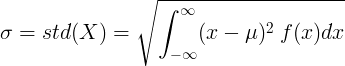
$\ سيغما = الأمراض المنقولة جنسيا (X) = \ sqrt {\ int _ {- \ infty} ^ {\ infty} (x- \ mu) ^ 2 \: f (x) dx}$

أو

$\ sigma = std (X) = \ sqrt {\ left [\ int _ {- \ infty} ^ {\ infty} x ^ 2 \: f (x) dx \ right] - \ mu ^ 2}$

الانحراف المعياري للمتغير العشوائي المنفصل

للمتغير العشوائي X المنفصل ذي القيمة المتوسطة μ ووظيفة الكتلة الاحتمالية P (x):

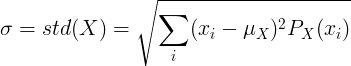
$\ sigma = std (X) = \ sqrt {\ sum_ {i} ^ {} (x_i- \ mu _X) ^ 2P_X (x_i)}$

أو

$\ sigma = std (X) = \ sqrt {\ left [\ sum_ {i} ^ {} x_i ^ 2P (x_i) \ right] - \ mu ^ 2}$

التوزيع الاحتمالي ►

أنظر أيضا

الاحتمالات والإحصاءات

جداول سريعة