e constant
La constant o número d'Euler és una constant matemàtica. La constant e és el nombre real i irracional.
e = 2.718281828459 ...
Definició de e
La constant e es defineix com el límit:
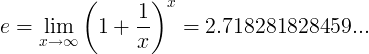
Definicions alternatives
La constant e es defineix com el límit:
![]()
La constant e es defineix com la sèrie infinita:
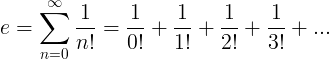
Propietats de e
Recíproc de e
El recíproc de e és el límit:
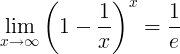
Derivats de e
La derivada de la funció exponencial és la funció exponencial:
( e x ) '= e x
La derivada de la funció de logaritme natural és la funció recíproca:
(log e x ) '= (ln x )' = 1 / x
Integrals d'e
La integral indefinida de la funció exponencial e x és la funció exponencial e x .
∫ e x dx = e x + c
La integral indefinida de la funció de logaritme natural log e x és:
∫ log e x dx = ∫ ln x dx = x ln x - x + c
La integral definida de 1 a e de la funció recíproca 1 / x és 1:
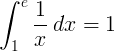
Logaritme de base i
El logaritme natural d'un nombre x es defineix com el logaritme e de base de x:
ln x = log e x
Funció exponencial
La funció exponencial es defineix com:
f ( x ) = exp ( x ) = e x
Fórmula d’Euler
El nombre complex e iθ té la identitat:
e iθ = cos ( θ ) + i sin ( θ )
i és la unitat imaginària (l'arrel quadrada de -1).
θ és qualsevol nombre real.
Vegeu també
- Com és 2.71828183?
- Regles del logaritme
- Logaritme natural
- Normes dels exponents
- Distribució normal
- Pi constant
- i constant - wikipedia