Regles d'exponent
Regles d'exponent, lleis de l'exponent i exemples.
Què és un exponent
La base a elevada a la potència de n és igual a la multiplicació de a, n vegades:
a n = a × a × ... × a
n vegades
a és la base i n és l'exponent.
Exemples
3 1 = 3
3 2 = 3 × 3 = 9
3 3 = 3 × 3 × 3 = 27
3 4 = 3 × 3 × 3 × 3 = 81
3 5 = 3 × 3 × 3 × 3 × 3 = 243
Regles i propietats dels exponents
| Nom de la regla | Regla | Exemple |
|---|---|---|
| Normes del producte | a n ⋅ a m = a n + m | 2 3 ⋅ 2 4 = 2 3 + 4 = 128 |
| a n ⋅ b n = ( a ⋅ b ) n | 3 2 ⋅ 4 2 = (3⋅4) 2 = 144 | |
| Regles del quocient | a n / a m = a n - m | 2 5 /2 3 = 2 5-3 = 4 |
| a n / b n = ( a / b ) n | 4 març / 2 3 = (4/2) 3 = 8 | |
| Regles de poder | ( b n ) m = b n⋅m | (2 3 ) 2 = 2 3⋅2 = 64 |
| b n m = b ( n m ) | 2 3 2 = 2 ( 3 2 ) = 512 | |
| m √ ( b n ) = b n / m | 2 √ (2 6 ) = 2 6/2 = 8 | |
| b 1 / n = n √ b | 8 1/3 = 3 √ 8 = 2 | |
| Exponents negatius | b -n = 1 / b n | 2 -3 = 1/2 3 = 0,125 |
| Regles zero | b 0 = 1 | 5 0 = 1 |
| 0 n = 0, per a n / 0 | 0 5 = 0 | |
| Una regla | b 1 = b | 5 1 = 5 |
| 1 n = 1 | 1 5 = 1 | |
| Menys una regla | 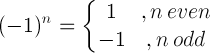 |
(-1) 5 = -1 |
| Regla derivada | ( x n ) ' = n ⋅ x n -1 | ( x 3 ) ' = 3⋅ x 3-1 |
| Regla integral | ∫ x n dx = x n +1 / ( n +1) + C | ∫ x 2 dx = x 2 + 1 / (2 + 1) + C |
Normes del producte dels exponents
Regla de producte amb la mateixa base
a n ⋅ a m = a n + m
Exemple:
2 3 ⋅ 2 4 = 2 3 + 4 = 2 7 = 2⋅2⋅2⋅2⋅2⋅2⋅2 = 128
Regla de producte amb el mateix exponent
a n ⋅ b n = ( a ⋅ b ) n
Exemple:
3 2 ⋅ 4 2 = (3⋅4) 2 = 12 2 = 12⋅12 = 144
Vegeu: Multiplicar exponents
Regles del quocient dels exponents
Regla del quocient amb la mateixa base
a n / a m = a n - m
Exemple:
2 5 /2 3 = 2 5-3 = 2 2 = 2⋅2 = 4
Regla del quocient amb el mateix exponent
a n / b n = ( a / b ) n
Exemple:
4 març / 2 3 = (4/2) 3 = 2 3 = 2⋅2⋅2 = 8
Vegeu: Dividir els exponents
Regles de poder dels exponents
Regla de poder I
( a n ) m = a n⋅m
Exemple:
(2 3 ) 2 = 2 3⋅2 = 2 6 = 2⋅2⋅2⋅2⋅2⋅2 = 64
Regla de poder II
a n m = a ( n m )
Exemple:
2 3 2 = 2 (3 2 ) = 2 (3⋅3) = 2 9 = 2⋅2⋅2⋅2⋅2⋅2⋅2⋅2⋅2 = 512
Regla de poder amb radicals
m √ ( a n ) = a n / m
Exemple:
2 √ (2 6 ) = 2 6/2 = 2 3 = 2⋅2⋅2 = 8
Regla dels exponents negatius
b -n = 1 / b n
Exemple:
2 -3 = 1/2 3 = 1 / (2⋅2⋅2) = 1/8 = 0,125
Vegeu: Exponents negatius
Vegeu també
- Afegir exponents
- Dividir els exponents
- Exponents fraccionaris
- Multiplicar exponents
- Exponents negatius
- Simplificar els exponents
- Exponent zero
- Calculadora d'exponent
- Calculadora de logaritmes
- Calculadora de creixement exponencial
- Calculadora anti-registre
- regles log (x)
- regles ln (x)
- e constant