Arccos (x) -toiminto
Arccos (x), cos -1 (x), käänteinen kosinifunktio .
Arccos-määritelmä
Luvun kaarikosinin x määritellään käänteinen kosini x: n funktiona, kun -1≤x≤1.
Kun y: n kosini on yhtä suuri kuin x:
cos y = x
Tällöin x: n arkosiini on yhtä suuri kuin x: n käänteinen kosinusfunktio, joka on yhtä suuri kuin y:
arccos x = cos -1 x = y
(Tässä cos -1 x tarkoittaa käänteistä kosinia eikä tarkoita kosinia -1: n voimalle).
Esimerkki
arccos 1 = cos -1 1 = 0 rad = 0 °
Kaavio arccoista
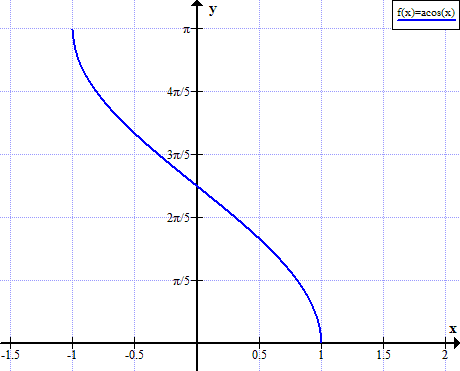
Arccos-säännöt
| Säännön nimi | Sääntö |
|---|---|
| Arkosiinin kosini | cos (arccos x ) = x |
| Kosinin arkosiini | arccos (cos x ) = x + 2 k π, kun k ∈ℤ ( k on kokonaisluku) |
| Negatiivisen argumentin arccot | arccos (- x ) = π - arccos x = 180 ° - arccos x |
| Täydentävät kulmat | arccos x = π / 2 - arcsin x = 90 ° - arcsin x |
| Arccos-summa | arccos ( α ) + arccos ( β ) = arccos ( αβ - √ (1- α 2 ) (1- β 2 ) ) |
| Arccos-ero | arccos ( α ) - arccos ( β ) = arccos ( αβ + √ (1- α 2 ) (1- β 2 ) ) |
| X: n synnin arccot | arccos (sin x ) = - x - (2 k +0,5) π |
| Arkososiinin sini | |
| Arkosiinin tangentti | 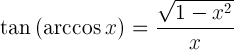 |
| Arkosiinin johdannainen | 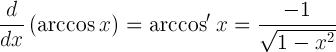 |
| Määrittelemätön arkosiinin integraali | |
Arccos-pöytä
| x | arccos (x) (rad) |
arccos (x) (°) |
|---|---|---|
| -1 | π | 180 ° |
| -√ 3 /2 | 5π / 6 | 150 ° |
| -√ 2 /2 | 3π / 4 | 135 ° |
| -1/2 | 2π / 3 | 120 ° |
| 0 | π / 2 | 90 ° |
| 1/2 | π / 3 | 60 ° |
| √ 2 /2 | π / 4 | 45 ° |
| √ 3 /2 | π / 6 | 30 ° |
| 1 | 0 | 0 ° |
Katso myös
- Kosinifunktio
- Arcsine-toiminto
- Arktinen toiminto
- Arccos-laskin
- Radiaanit asteina muunnin
- Arccot arvosta 0
- 1: n arccot
- 2: n arccot
- 3: n arccot
- Arccos of cos
- Arccos synnin
- Arccos-johdannainen
- Arccos-kaavio
- Cos of arccos
- Arccosin synti
- Arccos-ruskea