ई स्थिर

ई स्थिरांक या यूलर की संख्या एक गणितीय स्थिरांक है। ई स्थिरांक वास्तविक और अपरिमेय संख्या है।

e = 2.718281828459 ...

ई की परिभाषा
ई के गुण
आधार ई लघुगणक
घातांक प्रकार्य
यूलर का सूत्र

ई की परिभाषा

ई स्थिरांक को सीमा के रूप में परिभाषित किया गया है:

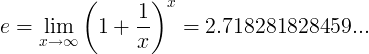
$e = \ lim_ {x \ rightarrow \ infty} \ left (1+ \ frac {1} {x} \ right) ^ x = 2.718281828459 ...$

वैकल्पिक परिभाषाएँ

ई स्थिरांक को सीमा के रूप में परिभाषित किया गया है:

$e = \ lim_ {x \ rightarrow 0} \ बाएँ (1+ \ दाएँ x) ^ \ frac {1} {}}$

ई स्थिरांक को अनंत श्रृंखला के रूप में परिभाषित किया गया है:

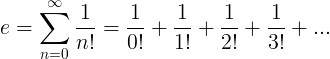
$e = \ sum_ {n = 0} ^ {\ infty} \ frac {1} {n!} = \ frac {1} {0!} + \ frac {1} {1!} + \ frac {1} { 2!} + \ frac {1} {3!} + ...$

ई के गुण

ई का पारस्परिक

ई का पारस्परिक सीमा है:

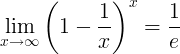
$\ lim_ {x \ rightarrow \ infty} \ बाएँ (1- \ frac {1} {x} \ right) ^ x = \ frac {1} {e}$

ई के डेरिवेटिव

घातीय फ़ंक्शन का व्युत्पन्न घातीय कार्य है:

( ई ^एक्स ) '= ई ^एक्स

प्राकृतिक लघुगणक फ़ंक्शन का व्युत्पन्न पारस्परिक कार्य है:

(log _e x ) '= (ln x )' = 1 / x

ई का अभिन्न अंग

के घातीय समारोह ई अनिश्चितकालीन अभिन्न ^एक्स घातीय समारोह ई है ^एक्स ।

∫ ई ^एक्स डीएक्स = ई ^एक्स + सी

प्राकृतिक लघुगणक फ़ंक्शन लॉग _ई x का अनिश्चितकालीन अभिन्न अंग है:

∫ log _e x dx = ∫ ln x dx = x ln x - x + c

पारस्परिक फ़ंक्शन 1 / x का 1 से e तक निश्चित अभिन्न है:

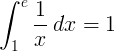
$\ int_ {1} ^ {e} \ frac {1} {x} \: dx = 1$

आधार ई लघुगणक

संख्या x के प्राकृतिक लघुगणक को x के आधार e लघुगणक के रूप में परिभाषित किया गया है:

ln x = log _e x

घातांक प्रकार्य

घातांक फ़ंक्शन को इस प्रकार परिभाषित किया गया है:

f ( x ) = exp ( x ) = e ^x

यूलर का सूत्र

जटिल संख्या e ⁱ की पहचान है:

ई ^iθ = cos ( θ ) + मैं पाप ( θ )

मैं काल्पनिक इकाई है (-1 का वर्गमूल)।

number कोई भी वास्तविक संख्या है।